Shortest path

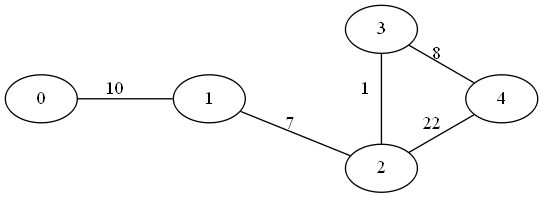
#include <iostream>
#include <tuple>
#include <algorithm>
#include <list>
#include <map>
#include <vector>
#include <limits>
using namespace std;

template<typename Type, typename ExtraData>
class MutableMinHeap {
  vector<tuple<size_t, Type, ExtraData>> data;
  map<size_t, size_t> positionMap;
  size_t progressiveIndex = -1;
public:
  // Inserts an element leaving the heap in a possibly invalid state
  // Returns an index that can be used to refer to the same node later
  size_t insertElementNoHeapify(Type weight, ExtraData extraData) {
    ++progressiveIndex;
    data.emplace_back(progressiveIndex, weight, extraData);
    positionMap[progressiveIndex] = data.size() - 1;
    return progressiveIndex;
  }
  void removeTopElementNoHeapify() {
    if (data.size() <= 0)
      throw runtime_error("No elements in the heap");
    size_t progrId = get<0>(data.front());
    swap(positionMap[get<0>(data[0])], positionMap[get<0>(data[data.size() - 1])]);
    swap(data[0], data[data.size() - 1]);
    positionMap.erase(progrId);
    data.resize(data.size() - 1);
  }
  void heapify() { // Reheapify through swimDown O(N)
    size_t currentNode = data.size();
    while (currentNode > 1) {
      // Set up indices for parent node and left/right nodes (if they exist)
      size_t parent = currentNode / 2;
      size_t left = parent * 2;
      left = (left <= data.size()) ? left - 1 : -1;
      size_t right = parent * 2 + 1;
      right = (right <= data.size()) ? right - 1 : -1;
      --parent;
      // Get the minimum in this subtree
      Type minimum = get<1>(data[parent]);
      size_t minElement = parent;
      if (left != -1 && get<1>(data[left]) < minimum)
        minElement = left;
      if (right != -1 && get<1>(data[right]) < minimum)
        minElement = right;
      if (minElement != parent) { // Swap and update indices
        swap(data[parent], data[minElement]);
        size_t s1 = get<0>(data[parent]);
        size_t s2 = get<0>(data[minElement]);
        swap(positionMap[s1], positionMap[s2]);
      }
      currentNode -= 2;
    }
  }
  tuple<size_t, Type, ExtraData>& getTopElement() {
    if (data.size() > 0)
      return data[0];
    else
      throw runtime_error("No elements in the heap");
  }
  // Access an element in the heap. If the weight is modified, a
  // reheapify will then be needed
  tuple<size_t, Type, ExtraData>& accessItem(size_t index) {
    return data[positionMap[index]];
  }
  bool empty() const {
    if (data.size() == 0)
      return true;
    else
      return false;
  }
  bool isElementInHeap(size_t index) {
    if (positionMap.find(index) == positionMap.end())
      return false;
    else
      return true;
  }
};

struct Edge {
  int v;
  int weight;
};

class Graph {
public:
  Graph(int V) {
    adjacencyList.resize(V);
    numberOfVertices = V;
    nodeIndices.resize(V);
    for (int i = 0; i < numberOfVertices; ++i) {
      nodeIndices[i] = heap.insertElementNoHeapify(numeric_limits<int>::max(), i);
      heapIndexToAdjIndex[nodeIndices[i]] = i;
    }
  }
  void addEdge(int u, int v, int w) {
    adjacencyList[u].push_back({ v, w });
  }
  void setStartPoint(int node) {
    startPoint = node;
  }
  void setEndPoint(int node) {
    endPoint = node;
  }

  vector<tuple<int, int, int>> getSP() {

    // Predecessor for every node in the optimal path
    vector<int> predecessor(numberOfVertices, -1);
    vector<int> minDist(numberOfVertices, numeric_limits<int>::max());

    // Start from root node
    auto& root = heap.accessItem(nodeIndices[startPoint]);
    get<1>(root) = 0;
    minDist[startPoint] = 0;
    heap.heapify(); // Reorder the heap

    while (heap.empty() == false) {
      // Get closest point on the fringe
      auto& closest = heap.getTopElement();

      if (get<1>(closest) == numeric_limits<int>::max())
        break; // Can't reach any other vertex

      if (get<0>(closest) == endPoint)
        break; // Found our destination

      // Update any adjacent vertex with a new path
      for (auto& e : adjacencyList[heapIndexToAdjIndex[get<0>(closest)]]) {

        if (minDist[e.v] > get<1>(closest) + e.weight) {
          auto& heapVertex = heap.accessItem(nodeIndices[e.v]);
          get<1>(heapVertex) = get<1>(closest) + e.weight;
          minDist[e.v] = get<1>(closest) + e.weight;
          predecessor[e.v] = heapIndexToAdjIndex[get<0>(closest)];
        }
      }

      // Remove it from the queue (i.e. visited)
      heap.removeTopElementNoHeapify();
      heap.heapify();
    }


    // Reconstruct the shortest path
    vector<tuple<int, int, int>> resultEdges; // u,v,w
    int cur = endPoint;
    int pred = predecessor[cur];
    while (pred != startPoint && pred != -1) {
      resultEdges.emplace_back(pred, cur, minDist[cur] - minDist[pred]);
      cur = predecessor[cur];
      pred = predecessor[cur];
    }
    resultEdges.emplace_back(startPoint, cur, minDist[cur] - minDist[startPoint]);

    return resultEdges;
  }


private:
  vector<list<Edge>> adjacencyList;
  int numberOfVertices;
  int startPoint, endPoint;
  MutableMinHeap<int, int> heap;
  vector<size_t> nodeIndices;
  map<size_t, int> heapIndexToAdjIndex;
};

int main() {

  Graph graph(5);
  graph.addEdge(0, 1, 10); // u,v,w
  graph.addEdge(1, 2, 7);
  graph.addEdge(2, 3, 1);
  graph.addEdge(3, 4, 8);
  graph.addEdge(2, 4, 22);

  graph.setStartPoint(0);
  graph.setEndPoint(4);

  auto res = graph.getSP();
  if (res.size() == 0 || get<2>(res[0]) == numeric_limits<int>::max()) {
    cout << "No shortest path exists" << endl;
    return 0;
  }
  cout << "Found shortest path from node " << 0 << " to node " << 4 << ":" << endl;
  for (auto& e : res)
    cout << "{" << get<0>(e) << ";" << get<1>(e) << "} with weight "
    << get<2>(e) << endl;

  return 0;
}