A tree in graph theory is an undirected acyclic connected graph. Common computer science tree-based structures like BSTs have trees as underlying graphs although they often define a root node and might define ordering criterions (thus actually rendering them directed graphs).

Finding the minimum spanning tree of a connected, undirected graph is one of the most famous problems in graph theory and has many practical applications ranging from network connections to cluster analysis and circuit design.

Kruskal, Prim and Boruvka are three common algorithms to solve MST problems.

Kruskal’s algorithm

Kruskal’s algorithm is a greedy MST finder. It works as follows

sort all edges of the graph ascending by their weight
chosen edges = []
for each edge in the graph until we have V-1 edges chosen
  let x,y be the nodes at the edge's ends
  if x and y aren't in the same component
    take the edge and set x and y to be in the same component

The termination condition is to have a MST of \( V-1 \) edges since the tree must connect all vertices together and no cycles can be formed.

Sorting all edges of the graph in order to grab each time the minimum weight one can be done with a classic ordering algorithm in \( O(n \log{n}) \) or with the help of a heap data structure.

It has to be noted that the bottleneck of the above algorithm isn’t the sorting but rather the comparison between the components each node belongs to (\( O(n^2) \) in a naive array assignment and update).

Union&Find disjoint set forests

By exploiting a particular data structure called disjoint set forest supporting two native operations (Union and Find) Kruskal’s algorithm can be consistently optimized.

The Find function is used to query the component a node belongs to (or the parent node of a component it belongs to). The Union function is used to mark two nodes as belonging in the same component.

The simplest data structure for a disjoint set forest is an array of parent nodes until the root of a component. Anyway if \( N \) nodes all belong to the same component and we search for the root node from the last one, it will take \( O(N) \) to find it.

A better data structure is an array of structures which contain the index of the parent node (i.e. the node associated with a component) and the rank of the tree rooted at a specific element.

struct Subcomponent {
  int parent;
  int rank;
};

Two optimization techniques are used when finding and unifying components:

Union by rank - to avoid deep trees being generated while unifying components, the component with a smaller tree is always appended to the root element of the component with a bigger tree. The term rank is different from depth or height of the tree since it just indicates how many times a same-rank join was performed for this component. Additionally when techniques like the second item of this list are used, the rank might not coincide with the height of a tree.
Path compression - Whenever an element is accessed, its hierarchy up to the root of the component is recursively set as children of the root. This flattens the tree and ensures a faster access to the root component next time a Find operation is called.

Let’s take for instance the following graph

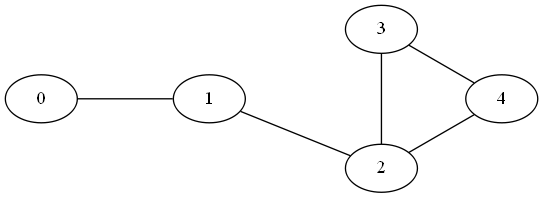
The following code uses a disjoint set forest data structure to detect cycles in the graph by recursively joining single-node components into a single one for the entire graph. If during an edge exploration two nodes are found to be already in the same component, a cycle is present.

#include <iostream>
#include <list>
#include <algorithm>
#include <vector>
using namespace std;

struct Subcomponent {
  int parent = -1;
  int rank = 0;
};

class Graph {
public:
  Graph(int V) {
    adjacencyList.resize(V);
    numberOfVertices = V;
  }
  void addEdge(int u, int v) {
    adjacencyList[u].push_back(v);
  }

  int findComponentFor(int node) {
    // Applies path compression to queries while searching for a root

    if (subcomponents[node].parent != node)
      subcomponents[node].parent = findComponentFor(subcomponents[node].parent);

    return subcomponents[node].parent;
  }
  
  void unionComponents(int node1, int node2) {
    int x = findComponentFor(node1);
    int y = findComponentFor(node2);

    if (x == y) return; // Already same component


    if (subcomponents[x].rank > subcomponents[y].rank)
      subcomponents[y].parent = x;
    else if (subcomponents[x].rank < subcomponents[y].rank)
      subcomponents[x].parent = y;
    else {
      subcomponents[x].parent = y;
      ++subcomponents[y].rank;
    }
  }

  bool checkForCycles() {
    subcomponents.clear();
    subcomponents.resize(numberOfVertices);
    {
      int i = -1;
      for_each(subcomponents.begin(), subcomponents.end(), [&](Subcomponent& el) {
        el.parent = ++i;
      });
    }

    for (int i = 0; i < adjacencyList.size(); ++i) {
      int j = -1;
      for (auto it = adjacencyList[i].begin(); it != adjacencyList[i].end(); ++it) {
        j = *it;

        int x = findComponentFor(i);
        int y = findComponentFor(j);

        cout << "Exploring edge {" << i << " - " << j << "}..." << endl;

        if (x == y) {
          cout << "Found cycle while exploring edge {" << i 
               << " - " << j << "}" << endl;
          return true;
        }

        unionComponents(i, j);
      }
    }
    return false;
  }

private:
  vector<list<int>> adjacencyList;
  int numberOfVertices;
  vector<Subcomponent> subcomponents;
};


int main() {

  Graph graph(5);
  graph.addEdge(0, 1);
  graph.addEdge(1, 2);
  graph.addEdge(2, 3);
  graph.addEdge(3, 4);
  graph.addEdge(2, 4);

  if (graph.checkForCycles())
    cout << "[Graph has cycles]" << endl;

  return 0;
}

Output

Exploring edge {0 - 1}...
Exploring edge {1 - 2}...
Exploring edge {2 - 3}...
Exploring edge {2 - 4}...
Exploring edge {3 - 4}...
Found cycle while exploring edge {3 - 4}
[Graph has cycles]

It has to be noted that, although every Find operation is in the order of \( O(\log{n}) \), this particular use of the disjoint set forest data structure for finding cycles in a graph isn’t particularly efficient since the overall complexity for all edges is \( O(E \log{V}) \). There are faster algorithms dedicated to the cycle-detection problem that by repeatedly performing DFS seeking back-edges in a running stack, achieve \( O(V + E) \).

The example above is provided as an easy and clear case of use for the disjoint set forest data structure.

Kruskal’s algorithm with disjoint set forest

As stated, by using the Union&Find algorithm based off the disjoint set forest data structure, Kruskal’s MST algorithm gains some performance in component node-ownership testing. The following code performs a search for the MST on the same graph as above augmented with edge weights

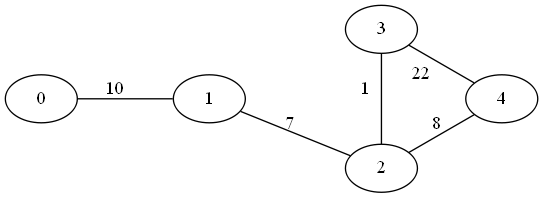
#include <iostream>
#include <tuple>
#include <algorithm>
#include <vector>
#include <type_traits>
using namespace std;

struct Subcomponent {
  int parent = -1;
  int rank = 0;
};

class Graph {
public:
  Graph(int V) {
    numberOfVertices = V;
  }
  void addEdge(int u, int v, int w) {
    adjacencyList.emplace_back(u, v, w);
  }

  int findComponentFor(int node) {
    // Applies path compression to queries while searching for a root

    if (subcomponents[node].parent != node)
      subcomponents[node].parent = findComponentFor(subcomponents[node].parent);

    return subcomponents[node].parent;
  }
  
  void unionComponents(int node1, int node2) {
    int x = findComponentFor(node1);
    int y = findComponentFor(node2);

    if (x == y) return; // Already same component


    if (subcomponents[x].rank > subcomponents[y].rank)
      subcomponents[y].parent = x;
    else if (subcomponents[x].rank < subcomponents[y].rank)
      subcomponents[x].parent = y;
    else {
      subcomponents[x].parent = y;
      ++subcomponents[y].rank;
    }
  }

  vector<tuple<int,int,int>> getMST() {

    // Initialize nodes to belong to single-node components

    subcomponents.clear();
    subcomponents.resize(numberOfVertices);
    {
      int i = -1;
      for_each(subcomponents.begin(), subcomponents.end(), [&](Subcomponent& el) {
        el.parent = ++i;
      });
    }
    
    // Sort all edges in ascending order (or use a heap)

    using Edge = tuple<int, int, int>;
    sort(adjacencyList.begin(), adjacencyList.end(), [](const Edge& a, const Edge& b) {
      if (get<2>(a) < get<2>(b))
        return true;
      else
        return false;
    });

    decltype(this->getMST()) result;
    for (Edge& t : adjacencyList) {
      int x = findComponentFor(get<0>(t));
      int y = findComponentFor(get<1>(t));

      if (x == y)
        continue;

      result.emplace_back(t);
      unionComponents(get<0>(t), get<1>(t));
      if (++edgeCount == numberOfVertices - 1) // Termination condition

        break;
    }

    return result;
  }

private:
  vector<tuple<int,int,int>> adjacencyList;
  int numberOfVertices;
  vector<Subcomponent> subcomponents;
};


int main() {

  Graph graph(5);
  graph.addEdge(0, 1, 10); // u,v,w

  graph.addEdge(1, 2, 7);
  graph.addEdge(2, 3, 1);
  graph.addEdge(3, 4, 22);
  graph.addEdge(2, 4, 8);

  auto res = graph.getMST();
  cout << "Found MST with the following edges:" << endl;
  for (auto& e : res)
    cout << "{" << get<0>(e) << ";" << get<1>(e) << "} with weight " 
         << get<2>(e) << endl;

  return 0;
}

Output

Found MST with the following edges:
{2;3} with weight 1
{1;2} with weight 7
{2;4} with weight 8
{0;1} with weight 10

As it can be seen from the output the algorithm excluded the most expensive edge since unnecessary to connect all the vertices of the tree. Even without the termination condition the algorithm would have avoided that edge since its vertices were already in the same component.

The runtime of the above algorithm is \( O(E \log{E}) \) or \( O(E \log{V}) \) depending on the greater factor between sorting and the union-find algorithm. In both cases a performance gain was achieved from the expected \( O(V^2) \).

Prim’s Algorithm

Prim’s algorithm works similarly to Kruskal’s but operates by keeping track of the minimum cut of the graph. Starting with the root node and going outwards, the fringe vertices’ edges are kept updated with the minimum cost to reach a vertex.

This process can be thought of as if a cost was assigned to each node not yet in the tree. The vertex with the minimum cost that can be reached is added to the MST and every new connection added by that vertex is compared against the old ones to find the minimum one to reach an external vertex.

costToReachNode[V] = +inf
costToReachNode[0] = 0 // Root node
for i in [0, V-1] // V nodes in MST
  node = getMinimumCostNodeNotInMSTyet(costToReachNode)
  add node to MST
  for every edge from node
    updateMinimumCosts(edge)

The code below features Prim’s algorithm on the same graph of the previous paragraph

#include <iostream>
#include <tuple>
#include <algorithm>
#include <list>
#include <map>
#include <vector>
#include <limits>
using namespace std;

template<typename Type, typename ExtraData>
class MutableMinHeap {
  vector<tuple<size_t, Type, ExtraData>> data;
  map<size_t, size_t> positionMap;
  size_t progressiveIndex = -1;
public:
  // Inserts an element leaving the heap in a possibly invalid state

  // Returns an index that can be used to refer to the same node later

  size_t insertElementNoHeapify(Type weight, ExtraData extraData) {
    ++progressiveIndex;
    data.emplace_back(progressiveIndex, weight, extraData);
    positionMap[progressiveIndex] = data.size() - 1;
    return progressiveIndex;
  }
  void removeTopElementNoHeapify() {
    if (data.size() <= 0)
      throw runtime_error("No elements in the heap");
    size_t progrId = get<0>(data.front());    
    swap(positionMap[get<0>(data[0])], positionMap[get<0>(data[data.size() - 1])]);
    swap(data[0], data[data.size() - 1]);
    positionMap.erase(progrId);
    data.resize(data.size() - 1);
  }
  void heapify() { // Reheapify through swimDown O(N)

    size_t currentNode = data.size();
    while (currentNode > 1) {
      // Set up indices for parent node and left/right nodes (if they exist)

      size_t parent = currentNode / 2;
      size_t left = parent * 2;
      left = (left <= data.size()) ? left - 1 : -1;
      size_t right = parent * 2 + 1;
      right = (right <= data.size()) ? right - 1 : -1;
      --parent;
      // Get the minimum in this subtree

      Type minimum = get<1>(data[parent]);
      size_t minElement = parent;
      if (left != -1 && get<1>(data[left]) < minimum)
        minElement = left;
      if (right != -1 && get<1>(data[right]) < minimum)
        minElement = right;
      if (minElement != parent) { // Swap and update indices

        swap(data[parent], data[minElement]);
        size_t s1 = get<0>(data[parent]);
        size_t s2 = get<0>(data[minElement]);
        swap(positionMap[s1], positionMap[s2]);
      }
      currentNode -= 2;
    }
  }
  tuple<size_t, Type, ExtraData>& getTopElement() {
    if (data.size() > 0)
      return data[0];
    else
      throw runtime_error("No elements in the heap");
  }
  // Access an element in the heap. If the weight is modified, a

  // reheapify will then be needed

  tuple<size_t, Type, ExtraData>& accessItem(size_t index) {
    return data[positionMap[index]];
  }
};

struct Edge {
  int v;
  int weight;
};

class Graph {
public:
  Graph(int V) {
    adjacencyList.resize(V);
    numberOfVertices = V;
    nodeIndices.resize(V);
    for (int i = 0; i < numberOfVertices; ++i) {
      nodeIndices[i] = heap.insertElementNoHeapify(numeric_limits<int>::max(), i);
      heapIndexToAdjIndex[nodeIndices[i]] = i;
    }
  }
  void addEdge(int u, int v, int w) {
    adjacencyList[u].push_back({ v, w });
  }

  vector<tuple<int, int, int>> getMST() {
    vector<bool> isNodeInMST(numberOfVertices, false);

    // Start from root node

    auto& root = heap.accessItem(nodeIndices[0]);
    get<1>(root) = 0;
    get<2>(root) = -1; // No parent

    heap.heapify();

    vector<tuple<int, int, int>> resultEdges; // u,v,w


    for (int i = 0; i < numberOfVertices; ++i) {
      // Pick the cheapest node to be reached

      auto& top = heap.getTopElement();

      // Store the path we followed to reach this node

      int nodeId = heapIndexToAdjIndex[get<0>(top)];
      int parent = get<2>(top);
      resultEdges.emplace_back(parent, nodeId, get<1>(top));

      isNodeInMST[nodeId] = true;
      heap.removeTopElementNoHeapify();      

      // Update every node that can be reached from this one

      // if we found a new cheapest cost to reach it

      for (auto it = adjacencyList[nodeId].begin();
        it != adjacencyList[nodeId].end(); ++it) {
        if (isNodeInMST[it->v] == false &&
          it->weight < get<1>(heap.accessItem(nodeIndices[it->v]))) {
          get<1>(heap.accessItem(nodeIndices[it->v])) = it->weight;
          get<2>(heap.accessItem(nodeIndices[it->v])) = nodeId;
        }
      }
      heap.heapify();
    }

    return resultEdges;
  }
  

private:
  vector<list<Edge>> adjacencyList;
  int numberOfVertices;
  MutableMinHeap<int, int> heap;
  vector<size_t> nodeIndices;
  map<size_t, int> heapIndexToAdjIndex;
};

Output

Found MST with the following edges:
{0;1} with weight 10
{1;2} with weight 7
{2;3} with weight 1
{2;4} with weight 8

The above algorithm uses a mutable minimum heap to achieve \( O(\log{V}) \) complexity for a node removal / update. Since the inner loop runs as for a BFS in \( O(V+E) \) the overall running time is \( O((V+E)\log{V}) \) which, for a connected graph where \( V = O(E) \), is \( O(E \log{V}) \). The code considerably grew in complexity though.

As a rule of thumb (there are no precise metrics as the best solution is usually to time performances on a case-to-case basis) Prim’s algorithm should be used when a graph is dense with lots of edges (since it mainly operates on vertices through the minimum cut) while Kruskal should be preferred when the graph is sparse i.e. with few edges and possibly many nodes.

Minimum spanning tree

Kruskal’s algorithm

Union&Find disjoint set forests

Kruskal’s algorithm with disjoint set forest

Prim’s Algorithm

References