Articulation points

Articulation points are of fundamental importance in many application fields since they provide a measure of the robustness of a network. A biconnected graph can sustain the loss of one node before power failing or being shut down / isolated in all or part of its subcomponents.

In the following graph there are two articulation points

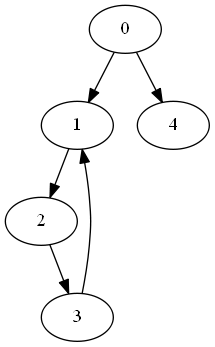
One is the root of the graph 0 and the other is the node 1. If any of these two were to be removed from the network, the graph would lose its weak connectivity.

Finding articulation points can surely be performed with a brute-force approach (i.e. disconnect one node and test for graph connectivity). That would cost \( O(V \cdot (V+E)) \). A better approach relies on the fact that back-edges make sure that any vertex in the stack of their ongoing search will not be an articulation vertex.

As in the case for the graph above two nodes can be articulation vertices:

• Root node with more than one children. A root node with just one child can be disconnected and the graph would simply be reduced to a new root.

• Non-root nodes whose subtree nodes have no back-edges to any of their ancestors (i.e. they’re the earliest ancestors for a set of nodes).

void findArticulationPoints() {

  int discoveryTimeGlobal = 0;
  vector<bool> APs(numberOfVertices, false);
  int root = 0; // 0 is the root node
  
  function<void(int)> recursiveSearchAP = [&](int node) {      

    data[node].visited = true;
    data[node].component = data[node].discoveryTime = discoveryTimeGlobal;
    ++discoveryTimeGlobal;

    for (auto adj : adjacencyList[node]) {

      if (data[adj].visited == false) {
        
        recursiveSearchAP(adj);

        data[node].component = min(data[node].component, data[adj].component);

        if (node == root && adjacencyList[node].size() > 1)
          APs[node] = true;
        else if (data[node].discoveryTime <= data[adj].component)
          APs[node] = true;

      } else {
        data[node].component = min(data[node].component, data[adj].discoveryTime);
      }
    }
  };

  for (int i = 0; i < numberOfVertices; ++i)
    recursiveSearchAP(i);

  cout << "Articulation points: { ";
  for (int i = 0; i < numberOfVertices; ++i) {
    if (APs[i] == true)
      cout << i << " ";
  }
  cout << "}" << endl;
}

The way the code above works is very similar to the strongly connected component search algorithm. The same considerations regarding discoveryTime hold. Complexity is \( O(V+E) \).