Connected components in graphs

Undirected graphs

For undirected graphs finding connected components is a simple matter of doing a DFS starting at each node in the graph and marking new reachable nodes as being within the same component.

A directed graph is connected if exists a path to reach a node from any other node, disconnected otherwise.

Let’s take for instance the following graph

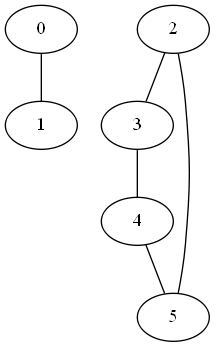
Since the graph is disconnected, it has connected subcomponents. The following code finds the connected components of the undirected graph

#include <iostream>
#include <list>
#include <vector>
using namespace std;

struct NodeData {
  int component = -1;
  bool visited = false;
};

class Graph {  
public:
  Graph(int V) {
    adjacencyList.resize(V);
    data.resize(V);
    numberOfVertices = V;
  }
  void addEdge(int u, int v) {
    adjacencyList[u].push_back(v);
    adjacencyList[v].push_back(u); // Undirected graph
  }

  void findConnectedComponents() {
    for (int i = 0; i < numberOfVertices; ++i) {
      dfsAndMark(i, i);
    }
    for (int i = 0; i < numberOfVertices; ++i) {
      cout << "Node " << i << " is in component " << 
        data[i].component << endl;
    }
  }

  // Execute a DFS from node and marks every encountered
  // node as belonging to component
  void dfsAndMark(int node, int component) {
    if (data[node].visited == true)
      return;
    data[node].component = component;
    data[node].visited = true;
    for (auto n : adjacencyList[node])
      dfsAndMark(n, component);
  }

private:
  vector<list<int>> adjacencyList;
  vector<NodeData> data;
  int numberOfVertices;
};


int main() {
  Graph graph(6);
  graph.addEdge(0, 1);
  graph.addEdge(2, 3);
  graph.addEdge(3, 4);
  graph.addEdge(4, 5);
  graph.addEdge(5, 2);

  graph.findConnectedComponents();

  return 0;
}

Node 0 is in component 0
Node 1 is in component 0
Node 2 is in component 2
Node 3 is in component 2
Node 4 is in component 2
Node 5 is in component 2

Directed graphs

In case of directed graphs an additional distinction has to be made:

As before a graph is said to be disconnected if it doesn’t exist a path from a start vertex to any other vertex. Not even ignoring the edge directions (see next point).
A directed graph is said to be weakly connected if ignoring all the directions (i.e. just considering the graph as an undirected one) results in a connected graph.

  bool weaklyConnected() { // Returns true if the DIRECTED graph is weakly connected

    // Ignore directions and check if every vertex is reachable
    // Agument connections with double edges
    auto oldAdjacencyList = adjacencyList;
    for (int i = 0; i < numberOfVertices; ++i)
      for (auto& c : oldAdjacencyList[i])
        adjacencyList[c].push_back(i);

    for (auto& d : data)
      d.visited = false;

    function<void(int)> dfsVisit = [&](int node) {
      if (data[node].visited == true)
        return;
      data[node].visited = true;
      for (auto n : adjacencyList[node])
        dfsVisit(n);
    };

    dfsVisit(0); // Mark every reachable vertex from the root

    // Check if every node has been reached and reset it to "unvisited"
    bool connected = true;
    for (auto& d : data) {
      if (d.visited == false)
        connected = false;
      else
        d.visited = false;
    }

    adjacencyList = oldAdjacencyList; // Restore old connections

    return connected;
  }

If the graph isn’t weakly connected, weak connected components can be found as in the case for the undirected graph, i.e. by just marking every node encountered from a starting vertex as being in the same component.

A directed graph is said to be strongly connected if from any node there’s always a path to reach any other one. This is the criterion city roads should be designed with.

An example is the following graph

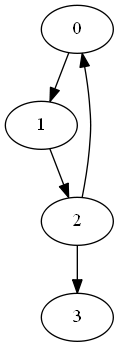
which, due to a missing path from 3 to any other node of the main cycle, is not strongly connected.

The way to check for a graph being strongly connected is doing a DFS from a starting node and check if every node can be reached. Then invert every edge in the graph and perform the same DFS from the same starting node again. If the graph is strongly connected every node will be reachable from the starting one and will also be capable of reaching it.

  bool stronglyConnected() {

    function<void(int)> dfsVisit = [&](int node) {
      if (data[node].visited == true)
        return;
      data[node].visited = true;
      for (auto n : adjacencyList[node])
        dfsVisit(n);
    };
    
    // 1) Try to reach every vertex from the root
    for (auto& d : data)
      d.visited = false;

    dfsVisit(0);

    // Check if every node has been reached and reset to "unvisited"
    bool connected = true;
    for (auto& d : data) {
      if (d.visited == false)
        connected = false;
      else
        d.visited = false;
    }

    if (connected == false)
      return false;

    // 2) Reverse every connection in the graph and try to reach
    // every vertex from the root again
    auto oldAdjacencyList = adjacencyList;
    adjacencyList.clear();
    adjacencyList.resize(numberOfVertices);
    for (int i = 0; i < numberOfVertices; ++i) {
      for (auto j : oldAdjacencyList[i])
        adjacencyList[j].push_back(i);
    }

    dfsVisit(0);

    // Check if every node has been reached and reset to "unvisited"
    connected = true;
    for (auto& d : data) {
      if (d.visited == false)
        connected = false;
      else
        d.visited = false;
    }

    adjacencyList = oldAdjacencyList; // Restore original connection

    return connected;
  }

Regarding identifying the strongly connected components, let’s take the following graph as an example. The start node is marked with a double circle

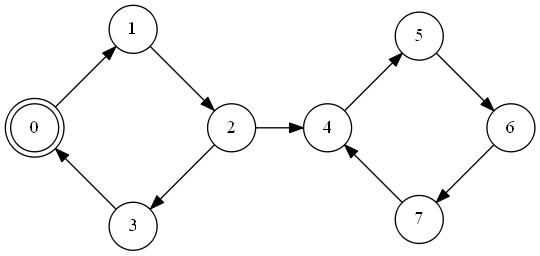
One of the most famous (although not the only one ~ cfr. Cormen) algorithms was discovered by Tarjan to find SCC (strongly connected components) in a graph. The indices of the nodes in the picture above represent discovery times, i.e. indices indicating when a node was discovered.

In the graph above the DFS proceeds in the following way:

0 is discovered
1 is discovered
2 is discovered
3 is discovered
a back edge to 0 is discovered. Node 3 is assigned the minimum between its component (the single-element 3 initially) and the back edge’s one (0). Therefore 3 gets 0 as belonging component.
Back from 3, 2 gets the minimum between its component 2 and 3’s findings: 0.
The process starts again from 4 being discovered.

void findStronglyConnectedComponents() {

    int discoveryTimeGlobal = 0;
    stack<int> currentComponent;

    function<void(int)> recursiveSearch = [&](int node) {

      // Assign a discovery time to each node and mark it as a single-node
      // component for this node
      data[node].discoveryTime = discoveryTimeGlobal;
      data[node].component = discoveryTimeGlobal;
      ++discoveryTimeGlobal;
      currentComponent.push(node); // Add it to the current component stack (useful
                                   // to track back and print the nodes in a component)
      data[node].onStack = true; // Set it on the stack (needed to check for cycles)
      data[node].visited = true;

      for (auto succ : adjacencyList[node]) {
        if (data[succ].visited == false) {
          // Not visited yet, recurse
          recursiveSearch(succ);
          // Grab the minimum found by my child
          data[node].component = min(data[node].component, data[succ].component);
        } else if (data[succ].onStack == true) { // Cycle found
          // *
          data[node].component = min(data[node].component, data[succ].discoveryTime);
        }
      }

      // If I'm still the root node
      if (data[node].component == data[node].discoveryTime) {
        // Generate a SSC with my stack
        cout << "Found SSC with nodes: { ";
        while (currentComponent.top() != node) { // I'm the beginning of this component
          cout << currentComponent.top() << " ";
          data[currentComponent.top()].onStack = false;
          currentComponent.pop();
        }
        cout << currentComponent.top() << " }" << endl;
        currentComponent.pop();
      }
    };

    for (auto& d : data)
      d.visited = false;

    for (int i = 0; i < numberOfVertices; ++i) {
      if (data[i].visited == false)
        recursiveSearch(i);
    } 
  }

Output:

Found SSC with nodes: { 7 6 5 4 }
Found SSC with nodes: { 3 2 1 0 }

It has to be noted that the line

data[node].component = min(data[node].component, data[succ].discoveryTime); // *

could also work if the back-edge’s component was used in the comparison rather than its discovery time. The reason why the discovery time is used instead it is because the back edge’s component value might not have been updated yet to a definitive value. For consistency reasons the component field indicates the earliest ancestor that can be reached from a node. Although, as stated, the algorithm would continue to work, the data regarding the individual component fields would be unreliable.

The complexity of the algorithm above, since it mainly calls DFS, it’s \( O(V+E) \) where \( V \) is the number of nodes of the graph and \( E \) the number of edges. DFS’s complexity, in fact, can be thought of as follows: node1 + edges_from_node1 + node2 + edges_from_node2 ... and rewritten as (node1 + node2 + node3 + node4 ..) + (edges_from_node1 + edges_from_node2 + ...) i.e. \( O(V+E) \). Notice that this complexity assumes an adjacency list as data structure (both nodes and edges are proportional to the input size). If we had to traverse an entire row to get the edges for a node (i.e. adjacency matrix) the complexity would be \( O(N^2) \).