Segment trees
Given the heights of N people waiting in a line and for each person the number of taller persons in front of him, find out their position in the line
E.g. for the following line
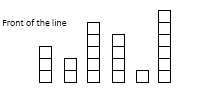
given the input data
heights = {6, 1, 2, 4, 3, 5}
in_front = {0, 4, 1, 1, 0, 0}
output
position_in_line = {3, 2, 5, 4, 1, 6}
A simple but extremely inefficient approach could be to just bruteforce each permutation in \( O(N!) \).
A better approach could be to order the input data by heights in ascending order: we can position the smallest element first since there are no smaller elements in the set that could be in front of it.
So we first can position the element 1 with 4 people in front of him
{ _ , _ , _ , _ , 1 , _ , _}
The second smallest element comes next: there’s one element in front of it and since we already positioned 1, no smaller elements will move it further behind
{ _ , 2 , _ , _ , 1 , _ , _}
and so on.
The problem with this approach is that sorting requires \( O(N \log(N)) \) and counting each time the free spaces from the beginning of the result vector makes the overall complexity \( O(N^2) \).
Segment trees
A segment tree is a data structure built as a full tree (a tree in which every node has either 0 or 2 children). Since the height of a binary tree is \( h = \lceil \log_2(N) \rceil \), the maximum number of nodes a full tree can be \( max = 2(2^h) -1 \).
The structure stores the results of an interval predicate in a heap-indexed-like vector. For a simple sum predicate (i.e. we’re interested in the sum of a given range of elements of the input set) we can build a segment tree in \( O(N) \) and query the value of the predicate in a given interval \( [x;y] \) in \( O(\log(N)) \). Updating is also \( O(\log(N)) \).
inline int mid(int left, int right) {
return (left + right) / 2;
}
vector<int> build_segment_tree(const vector<int>& input) {
// A segment tree is a full tree and has
// h = ceil(log2(N))
// max number of nodes: 2 * (2^h) - 1
const int h = (int)ceil(log2(input.size()));
vector<int> st(2 * (int)pow(2, h) - 1);
function<int(int, int, int)> build_st = [&](int i, int left, int right) {
if (left == right) {
st[i] = input[left];
return st[i];
}
auto m = mid(left, right);
int sum_left = build_st(2 * i + 1, left, m);
int sum_right = build_st(2 * i + 2, m + 1, right);
st[i] = sum_left + sum_right;
return st[i];
};
build_st(0, 0, (int)input.size() - 1);
return st;
}
int segment_tree_get_range(const vector<int>& st, const int st_left, const int st_right, int query_left, int query_right) {
function<int(int, int, int)> query_st = [&](int i, int node_left, int node_right) {
if (query_left > node_right || query_right < node_left)
return 0;
if (node_left >= query_left && node_right <= query_right)
return st[i];
auto m = mid(node_left, node_right);
return query_st(2 * i + 1, node_left, m) + query_st(2 * i + 2, m + 1, node_right);
};
return query_st(0, st_left, st_right);
}
void update_segment_tree_element(vector<int>& input, const int node_i, const int value, vector<int>& st, const int st_left, const int st_right) {
int diff = value - input[node_i];
function<void(int, int, int)> update_st = [&](int i, int node_left, int node_right) {
if (node_i > node_right || node_i < node_left)
return;
if (node_i >= node_left && node_i <= node_right)
st[i] += diff; // (1)
if (node_left != node_right) { // Termination condition, (1) is executed. This one isn't
auto m = mid(node_left, node_right);
update_st(2 * i + 1, node_left, m);
update_st(2 * i + 2, m + 1, node_right);
}
};
input[node_i] = value;
update_st(0, st_left, st_right);
}Given these tools the algorithm becomes pretty straightforward
vector<int> calculate_pos_in_line(vector<int> &heights, vector<int> &in_front) {
vector<pair<int, int>> vals;
for (int i = 0; i < heights.size(); ++i) {
vals.emplace_back(heights[i], in_front[i]);
}
sort(vals.begin(), vals.end(), [](const pair<int, int>& e1, const pair<int, int>& e2) {
return e1.first <= e2.first;
});
vector<int> res(vals.size(), -1);
vector<int> spots(vals.size(), 1); // 1 means 'available'
auto stree = build_segment_tree(spots);
function<int(const vector<int>&, const int, int, int, int)> find_sum_in_st = [&](const vector<int>& st, const int sum, int i, int range_begin, int range_end) {
if (range_begin == range_end)
return range_begin; // Reached leaf
int i_elements = st[i];
int lower_half_elements = st[2 * i + 1];
auto m = mid(range_begin, range_end);
if (lower_half_elements < sum)
return find_sum_in_st(st, sum - lower_half_elements, 2 * i + 2, m + 1, range_end);
else
return find_sum_in_st(st, sum, 2 * i + 1, range_begin, m);
};
for (int i = 0; i < vals.size(); ++i) {
int pos = vals[i].second;
int range_begin = 0, range_end = (int)vals.size() - 1;
auto p = find_sum_in_st(stree, pos + 1, 0, range_begin, range_end);
res[p] = vals[i].first;
update_segment_tree_element(spots, p, 0, stree, 0, (int)spots.size() - 1);
}
return res;
}A driver for the code above follows
int main() {
vector<int> heights = { 6, 1, 2, 4, 3, 5 };
vector<int> in_front = { 0, 4, 1, 1, 0, 0 };
auto position_in_line = calculate_pos_in_line(heights, in_front);
// ..
}