Pattern matching
Pattern matching is often required in a large variety of problems and diverse input data. The most common computer science instance of this problem occurs in string searching. Single pattern algorithms are used to identify the position of a pattern into a text or to yield if the pattern was not found.
The naive way of solving this problem is a \( O((n-m)m) \) algorithm which just tries to match the pattern repeatedly on the input text. There are many other algorithms which prove to be more efficient in this task. Arguably three of the most famous ones are
Knuth-Morris-Pratt
Knuth-Morris-Pratt algorithm (KMP) uses a DFA - Deterministic Finite Automaton to achieve string pattern matching in linear time. A preprocessing step where the DFA is actually constructed is necessary. Given a pattern of length \( m \) and a text of length \( n \), KMP is \( O(m+n) \).
int kmp(const string& text, const string& pattern) {
if (pattern.size() <= 0)
return 0;
vector<vector<int>> dfa(pattern.size() + 1, vector<int>(256, 0));
int X0 = 0;
int pattern_index = -1;
int dfa_index = -1;
// DFA construction step
while (pattern_index < static_cast<int>(pattern.size())) {
dfa[++dfa_index] = dfa[X0];
X0 = dfa[X0][pattern[++pattern_index]];
dfa[dfa_index][pattern[pattern_index]] = dfa_index + 1;
}
int pos = 0;
for (int i = 0; i < text.size(); ++i) {
pos = dfa[pos][text[i]];
if (pos == pattern.size())
return static_cast<int>(i + 1 - pattern.size());
}
return -1;
}The DFA is constructed by storing a backup position X0 to recover the matching state in case a previously-covered character is encountered again. This ensures the DFA isn’t completely reset to its starting position if a partial matching is found. A simple DFA for the text Hi follows
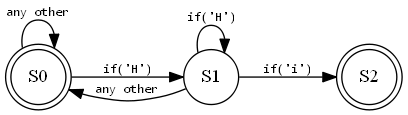
If the alphabet is small (e.g. DNA bases) there’s a high chance that reusable subpatterns will be present and thus it is likely KMP will outperform other algorithms.
Boyer-Moore
Boyer-Moore algorithm also features a preprocessing step although considerably more lightweight than building an entire DFA as in KMP. A skipping-table is computed to determine how much can the algorithm skip if a mismatch with a character actually contained in the pattern is encountered. It acts as a quick way to find a synchronization point.
int bm(const string& text, const string& pattern) {
if (pattern.size() <= 0)
return 0;
vector<int> rightmostPosition(256, -1);
for (int i = 0; i<pattern.size(); ++i)
rightmostPosition[pattern[i]] = i;
int pos = 0;
while (pos + pattern.size() - 1 < text.size()) {
bool match = true;
for (int i = static_cast<int>(pattern.size() - 1); i >= 0; --i) {
if (pattern[i] != text[pos + i]) {
match = false;
int rightmost = rightmostPosition[text[pos + i]];
if (rightmost == -1)
pos = pos + i + 1;
else {
if (rightmost > i)
++pos;
else
pos = pos + (i - rightmost);
}
break;
}
}
if (match)
return pos;
}
return -1;
}Long search patterns can take advantage of how skipping parts of the text works and considerably speed it up also for all-points searching; although worst-case execution time is \( \Theta(mn) \) in case input and pattern solely consist of a single character, the Galil rule avoids recomparing characters already known to match to achieve \( O(n+n) \) in both single and multi search mode.
Rabin-Karp
Rabin-Karp uses an entirely different approach based on hashing the pattern and a running portion of the text. Given a pattern and an input text the pattern is first hashed and the result stored, then a running hash is kept through all the input text to be compared with the stored pattern hash.
int rk(const string& text, const string& pattern) {
if (pattern.size() <= 0 || text.size() < pattern.size())
return -1;
unsigned int k = 1117; // Prime
unsigned long long patternHash = 0;
for (const auto& c : pattern)
patternHash = ((patternHash * k) + c) % k;
auto checkMatch = [&](int pos, unsigned long long hash) {
if (hash == patternHash) {
for (int i = 0; i<pattern.size(); ++i) {
if (pattern[i] != text[pos + i])
return false;
}
return true;
}
return false;
};
unsigned long long runningHash = 0;
for (int i = 0; i<pattern.size(); ++i)
runningHash = ((runningHash * k) + text[i]) % k;
if (checkMatch(0, runningHash))
return 0;
for (int i = 1; i + (pattern.size() - 1) < text.size(); ++i) {
runningHash = (runningHash - text[i - 1] * (k * (pattern.size() - 1))) % k;
runningHash = ((runningHash * k) + text[i + (pattern.size() - 1)]) % k;
if (checkMatch(i, runningHash))
return i;
}
return -1;
}Rabin-Karp’s efficiency depends on the efficient computation of hash values. The example above features a simple Rabin fingerprint hash function. Average case is \( O(n+m) \). Depending on the hash function used a worst-case of \( O(nm) \) might be possible.
Collisions cannot be avoided (although careful tuning might significantly reduce these issues) therefore a string comparison verification is needed once a matching hash is found. The code above works since deleting the first most-significant digit and adding the last least-significant digit in
runningHash = (runningHash - text[i - 1] * (k * (pattern.size() - 1))) % k;
runningHash = ((runningHash * k) + text[i + (pattern.size() - 1)]) % k;ensures the hash can still be compared to the stored pattern one. Given \( a \mod k = r \) and \( a = kq + r \) where \( q \) is the quotient, it holds
\[((a \mod k) \cdot k + b) \mod k = ((a-k \cdot q) \cdot k + b) \mod k \\= (a \cdot k + b -k \cdot q \cdot k) \mod k = (a \cdot k + b) \mod k\]The last passage is made possible by the fact that \( a \mod k = (a + nk) \mod k, \forall n \).
Therefore
\[((a \mod k) \cdot k + b) \mod k = (a \cdot k + b) \mod k\]A programming-related caveat: one should not confuse the modulo operator with C++’s division remainder % operator which abides by the following
(a / b) * b + a % b == a (with b != 0)
[expr.mul]/p4
The binary / operator yields the quotient, and the binary % operator yields the remainder from the division of the first expression by the second. If the second operand of / or % is zero the behavior is undefined. For integral operands the / operator yields the algebraic quotient with any fractional part discarded;[…] if the quotient a/b is representable in the type of the result, (a/b)*b + a%b is equal to a; otherwise, the behavior of both a/b and a%b is undefined.
References
- Dan Gusfield - Algorithms on Strings, Trees and Sequences
- Q1413514 on modulo equality
- The C++ standard