In computer science the so-called optimal binary search tree problem consists in finding the binary search tree which guarantees the minimum possible search time for each of its nodes given an access-frequency or access-probability vector.

Suppose we have two nodes of value 10 and 20. These two nodes can form the following binary search trees

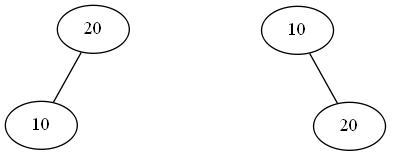
now suppose we also have an array of access frequencies per each node. This tells us that the node 10 will be accessed 50 times while the node 20 will be accessed 100 times.

If we were to access the nodes in a sequential fashion we would just put the node 20 (with the highest access frequency) at the front and the other node at the bottom (less accessed). Anyway with binary trees we would ideally like to have the node 20, which is the most-accessed one, as root in order to reduce searching.

In the case above we have two possible BSTs. Weighing more deeply nested nodes more, the first will have cost

while the second BST will have cost

This leads us to state that the optimal binary search tree is the first one with the most-accessed node at the root.

A recursive solution

If the input nodes are sorted (condicio sine qua non) a recursive algorithm can be set up to solve the problem. Let us consider again the two BSTs above

In the first case we chose 20 as root and 10 as subnode. There could have been other subnodes as well. The key to solve the problem is to consider the way we assigned the weights:

we weighed 1 the root node’s frequency and 2 the other node’s frequency. This is equivalent to doing

and thus a recursive relation such as

costOfTree(root) = sum_of_all_frequencies_in_tree(root) +
                   costOfTree(root->left) +
                   costOfTree(root->right);

would give us the cost of a specific subtree rooted at root. What we need to do is iterate over all the possible root nodes (i.e. try each node as root) for every possible subtree.

costOfTree(root) {
  minCost = +inf
  foreach node
    root = node
    newCost = sum_of_all_frequencies_in_tree(root) +
              costOfTree(root->left) +
              costOfTree(root->right)
    minCost = min(minCost, newCost)

  return minCost
}

A careful reader might notice that we haven’t dealt with the correctness of a BST in any way, i.e. we didn’t care of having lesser nodes in the left subtree and bigger nodes in the right subtree. The pseudocode above only works if the nodes are sorted since grabbing each node and considering it as root and recursing on the left and right parts of the input nodes array only yields valid BSTs if the nodes are sorted (and so must be the frequencies to have a consistent access). A snippet to sort frequencies and nodes according to the nodes’ ordering follows

vector<int> nodes = { 20,  10 };
vector<int> freqs = { 100, 50 };

// Sort nodes and arrange frequencies accordingly
vector<pair<int, int>> indices;
for (int i = 0; i < nodes.size(); ++i) {
  indices.emplace_back(make_pair(i, nodes[i]));
}
auto sortByNodes = [](const pair<int, int>& a,
                      const pair<int, int>& b) {
  if (a.second < b.second)
    return true;
  else
    return false;
};
sort(indices.begin(), indices.end(), sortByNodes);
vector<int> output;
for (int i = 0; i < indices.size(); ++i) {
  output.push_back(freqs[indices[i].first]);
  nodes[i] = indices[i].second;
}
freqs = std::move(output);

Dynamic programming solution

The pseudocode proposed above has \( O(2^N) \)exponential complexity since once a root has been established, it tries to build recursively all possible subtrees and the process starts again by testing each node as root.

Since recursively testing for all possible subtrees has the overlapping subproblems property (i.e. we’re computing the same problem over and over) and since for every subset of items (e.g. only 2 nodes) an optimal minimum cost solution can be found, the problem has the optimal substructure property as well and thus it is a good candidate to be solved via dynamic programming.

The following code puts together the requirement for the keys array (i.e. the array of nodes) to be sorted, along with the frequencies arranged abiding by their order, and a dynamic programming iteration via increasing subsets.

#include <iostream>
#include <vector>
#include <limits>
#include <algorithm>

void sortNodesAndFrequenciesByNodes(std::vector<int>& nodes,
                                    std::vector<int>& freqs) {
  // Sort nodes and arrange frequencies accordingly
  std::vector<std::pair<int, int>> indices;
  for (int i = 0; i < nodes.size(); ++i) {
    indices.emplace_back(std::make_pair(i, nodes[i]));
  }
  auto sortByNodes = [](const std::pair<int, int>& a,
    const std::pair<int, int>& b) {
    if (a.second < b.second)
      return true;
    else
      return false;
  };
  std::sort(indices.begin(), indices.end(), sortByNodes);
  std::vector<int> output;
  for (int i = 0; i < indices.size(); ++i) {
    output.push_back(freqs[indices[i].first]);
    nodes[i] = indices[i].second;
  }
  freqs = std::move(output);
}

int minimumCostBST(std::vector<int>& nodes, std::vector<int>& freqs) {

  // A memoization matrix of NxN
  const size_t N = nodes.size();
  std::vector<std::vector<int>> matrix(N, std::vector<int>(N, 0));

  // Base cases: 1-length subexpressions
  for (int i = 0; i < N; ++i) {
    matrix[i][i] = freqs[i];
  }

  // For every subexpression length
  for (int l = 2; l <= N; ++l) {
    for (int i = 0; i <= N - l; ++i) { // For every beginning i
      int j = i + l - 1; // And get the subexpression ending too

      int freqsSum = 0;
      for (int k = i; k <= j; ++k)
        freqsSum += freqs[k]; // This might also be cached

      int minFound = std::numeric_limits<int>::max();

      for (int r = i; r <= j; ++r) {

        int leftCost = 0, rightCost = 0;
        if (r - 1 >= i)
          leftCost = matrix[i][r - 1];
        if (r + 1 <= j)
          rightCost = matrix[r + 1][j];

        int newMin = freqsSum + leftCost + rightCost;

        if (newMin < minFound)
          minFound = newMin;
      }

      // Store the minimum obtained for this interval
      matrix[i][j] = minFound;
    }
  }

  return matrix[0][N - 1];
}

int main() {
  std::vector<int> nodes = { 15, 12, 20 };
  std::vector<int> freqs = { 31, 8, 50 };

  sortNodesAndFrequenciesByNodes(nodes, freqs); // Necessary passage

  std::cout << "Optimal binary search tree has cost "
    << minimumCostBST(nodes, freqs); // 136

  return 0;
}

This algorithm has complexity \( O(N^3) \) and features optimization spots, for instance frequencies sums could be cached instead of being recalculated each time.