Write an efficient algorithm to count how many subarrays sum to an even value in a given array

Solution I

Trivial solution: cycling through the array in \( O(N^2) \)

int evenSumSubarrays(const vector<int>& vec) {
  int even = 0;
  for (auto i = vec.begin(), ie = vec.end(); i != ie; ++i) {
    for (auto j = i + 1;; ++j) {
      even += (accumulate(i, j, 0) % 2 == 0);
      if (j == vec.end()) break;
    }
  }
  return even;
}

Solution II

Before diving into the code, some mathematical observations have to be made. First off we should realize that adding two odd numbers always equal an even one and the same holds when adding two even numbers. Adding an odd number to an even number won’t work.

Let us consider the input vector {2, 7, 4, 1} and link with an edge two nodes whose sum will be equal to an even number

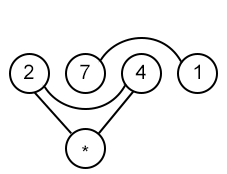
2 and 4 already count singularly as even-sum subarrays, therefore a virtual node was added to ensure an additional edge is present for every even number in the array. 2 and 4 are also connected with each other since they’re both even. Even numbers are therefore accounted both singularly and together. Odd numbers are linked together as well since the sum of two odd numbers is even. The key to understanding this solution is realizing that every number added either increments the number of edges between even numbers (if even) or adds another edge linked to the most recent odd number encountered (if odd).

Even nodes form a fully connected subgraph and so do odds. Therefore the number of edges for a fully connected graph is

This can also intuitively be calculated via triangular numbers considering the fact that given \( N \) nodes numbered from 1 to \( N \), the first node is linked to \( N-1 \) other nodes, the second one to \( N-2 \) other nodes, etc.. therefore yielding the same amount. We can therefore linearly count the number of even-sum subarrays as follows

int evenSumSubarrays(const vector<int>& vec) {
  int sum = 0, odds = 0, evens = 1; // Insert a virtual node
  for (auto it = vec.begin(), ie = vec.end(); it != ie; ++it) {
    sum = (sum + *it) % 2;
    (sum == 0) ? ++evens : ++odds;
  }
  return (evens * (evens - 1) / 2) + (odds * (odds - 1) / 2);
}

The above code runs in \( O(N) \).