Estimate the number of times the fn() function gets called in the following code

for (int i = 0; i < N; ++i) {
  for (int j = 0; j < i; ++j) {
    fn();
    for (int k = i + 1; k < N; ++k) {
      fn();
    }
  }
}

Let’s start by breaking this up into pieces.

A simple loop would count up to $ N $, while the first two loops

for (int i = 0; i < N; ++i) {
  for (int j = 0; j < i; ++j) {
    fn();
  }
}

will generate a series of values as follows

0 1 2 3 4 5 ..

this is a simple triangular number whose partial sum is given by

\[\sum_{k=1}^n k = \frac{n(n+1)}{2}\]

Proof

Let
\[S = 1 + 2 + ... + (n - 1) + n \\ S = n + (n-1) + ... + 2 + 1\]
adding these two equivalent equations gives us
\[2S = (n+1) + (n+1) + ... + (n+1) + (n+1) = n(n+1)\]
therefore $ S = \frac{n(n+1)}{2} $

We now have the first part of our result: fn() is called $ \frac{n(n+1)}{2} $ times in its outmost invocation.

Actually since the first iteration is not executed (i.e. no inner loop will take place for i == 0), the real number of times the first invocation of fn() is executed is $ \frac{(n-1)(n-1 + 1)}{2} $. For simplicity’s sake we’ll do our math considering the first iterations to be executed as well.

The most inner loop calculation is somewhat trickier to get right. First it is important to realize that the loop index k only depends on the outer loop index i (and not on j) although it will be executed j times for each invocation.

The following graph summarizes the times the inner fn() call is performed

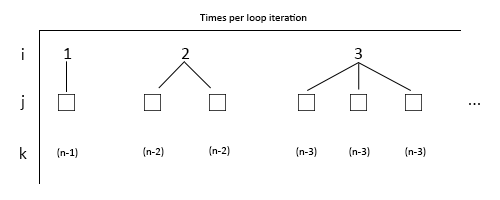
Since the innermost loop index goes from i + 1 to N, it is straightforward to realize that the innermost invocations of fn() are given by the sequence

\[1 \cdot (n-1) + 2 \cdot (n-2) + 3 \cdot (n-3) ... (n-1) \cdot (n - (n-1))\]

which is equivalent to

\[n - 1 + 2n - 4 + 3n - 9 + ... + (n-1) = n\sum_{i=1}^{n-1}{i} - \sum_{i=1}^{n-1}{i^2}\]

The first term is again $ \frac{n(n-1)}{2} $ while the second one is the sum of the first $ n-1 $ squares.

The sum of a sequence of squares has a partial sum

\[\sum_{i \mathop = 1}^n i^2 = \frac {n \left({n + 1}\right) \left({2 n + 1}\right)} 6\]

Proof

By mathematical induction we can prove that iff

$ P(1) $ is true [base case]

for any $ P(k) $ that is true, it follows that $ P(k+1) $ is also true [induction step]

then the theorem is verified. Therefore

for $ n = 1 $ we have $ \frac {n \left({n + 1}\right) \left({2 n + 1}\right)} 6 = \frac {1 \left({1 + 1}\right) \left({2 \cdot 1 + 1}\right)} 6 = \frac 6 6 = 1 $ so $ P(1) $ is true

assuming $ P(k) $ holds, then also our $ P(k+1) $ must hold.

We have
\[\begin{align} P(k) \Rightarrow & \sum_{i \mathop = 1}^k i^2 = \frac {k \left({k + 1}\right) \left({2 k + 1}\right)} 6 \\ P(k+1) \Rightarrow & \sum_{i \mathop = 1}^{k+1} i^2 = \frac{\left({k+1}\right) \left({k+2}\right) \left({2 \left({k+1}\right) + 1}\right)} 6 \end{align}\]
using the properties of summation we have $\sum_{i \mathop = 1}^{k+1} i^2 = \sum_{i \mathop = 1}^k i^2 + \left({k+1}\right)^2$ expanding and calculating the RHS we get
\[\sum_{i \mathop = 1}^{k+1} i^2 = \frac{\left({k + 1}\right) \left({k + 2}\right) \left({2 \left({k + 1}\right) + 1}\right)} 6\]
If follows that when $ P(k) $ holds, also $ P(k+1) $ holds.
\[\tag*{$\blacksquare$}\]

We can conclude that the inner fn() is executed

\[n \left[ \frac{n(n-1)}{2} \right] - \frac {n \left({n + 1}\right) \left({2 n + 1}\right)} 6\]

times.

The total number of times fn() is executed in the code provided also keeping in mind that the first iteration isn’t executed by the inner loops is therefore equal to

\[f(n) = \frac{(n-1)n}{2} + \left\{ (n-1) \left[ \frac{(n-2)(n-1)}{2} \right] - \frac { (n-2) \left({n - 1}\right) \left[ 2 (n - 2) + 1 \right]} 6 \right\}\]

For n = 100, $ f(100) = 166650 $ invocations. The algorithm is $ O(N^3) $.

References

Compendium of mathematical proofs and Wikipedia