Maximum flow and bipartite matching

The maximum flow problem involves finding a flow through a network connecting a source to a sink node which is also the maximum possible. Applications of this problem are manifold from network circulation to traffic control.

The Ford-Fulkerson algorithm is commonly used to calculate the maximum flow on a given graph although a variant called Edmonds-Karp ensures the maximum flow is computed in \( O(V E^2) \) (or \( O(V^2) \) in case an adjacency matrix is used).

Given the following graph

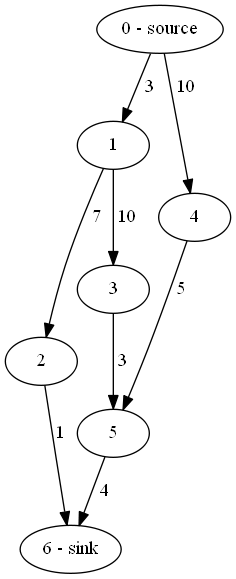
the maximum flow through the network is constrained by the minimum cut passing through the edges directly linked to the sink node. Therefore the maximum flow on the network is 5.

Edmonds-Karp uses breadth-first search as follows

find all paths from source to sink with BFS
for each path
  find the maximum flow that can flow through that path
  augment the path and increase the total flow

Augmenting a path means saturating its capacity \( c \) with a running flow \( f_p \le c \). The following code implements Edmonds-Karp with an adjacency list on the graph of the previous image

#include <iostream>
#include <vector>
#include <list>
#include <queue>
using namespace std;

struct Edge {
  int u; // Origin
  int v; // Destination
  int weight; // Capacity
  int flux; // Current flux
};

class Graph {
public:
  Graph(int V) : source(-1), sink(-1) {
    adjacencyList.resize(V);
    numberOfVertices = V;
  }
  void addEdge(int u, int v, int w) {
    adjacencyList[u].push_back({ u, v, w, 0 });
  }
  void setSource(int s) {
    source = s;
  }
  void setSink(int s) {
    sink = s;
  }

  int maximumFlow() { // Edmonds–Karp

    int maximumFlow = 0;
    vector<Edge*> parentEdges(numberOfVertices, nullptr);
    deque<int> bfsQueue;

    // Do a BFS to find every path from source to sink
    bfsQueue.push_back(source);
    while (bfsQueue.empty() == false) {

      int current = bfsQueue.front();
      bfsQueue.pop_front();
      for (auto& edge : adjacencyList[current]) {

        parentEdges[edge.v] = &edge;
        bfsQueue.push_back(edge.v);

        if (edge.v == sink) {

          // A path was found from source to sink
          // Find the maximum flow on this path
          int maxFlow = numeric_limits<int>::max();
          auto parentEdge = parentEdges[edge.v];
          while (parentEdge != nullptr) {
            maxFlow = min(maxFlow, parentEdge->weight - parentEdge->flux);
            parentEdge = parentEdges[parentEdge->u];
          }

          maximumFlow += maxFlow;

          // Augment the entire path
          parentEdge = parentEdges[edge.v];
          while (parentEdge != nullptr) {
            parentEdge->flux += maxFlow;
            parentEdge = parentEdges[parentEdge->u];
          }
        }
      }
    }
    return maximumFlow;
  }

private:
  vector<list<Edge>> adjacencyList;
  int numberOfVertices;
  int source, sink;
};


int main() {

  Graph graph(7);
  graph.addEdge(0, 1, 3);
  graph.addEdge(0, 4, 10);
  graph.addEdge(1, 3, 10);
  graph.addEdge(1, 2, 7);
  graph.addEdge(4, 5, 5);
  graph.addEdge(5, 6, 4);
  graph.addEdge(2, 6, 1);

  graph.setSource(0);
  graph.setSink(6);

  cout << "Maximum flow: " << graph.maximumFlow(); // 5

  return 0;
}

Bipartite Matching

A bipartite graph is a graph whose vertices can be divided into two independent sets such that every edge \( (u,v) \) either \( u \) belongs to the first one and \( v \) to the second one or vice versa. A bipartite graph satisfies the graph coloring condition, i.e. has no odd-length cycles. Bipartite matching is the problem of finding a subgraph in a bipartite graph where no two edges share an endpoint.

An example is the following graph

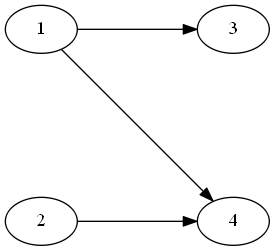
each edge has a weight of 1 although different weights could also be used to indicate the fitness of a particular node of the left set for a node in the right set (e.g. job fitness / skills / affinity). The same maximum flow algorithm can also be used to find the bipartite matching graph since it coincides with the maximum flow through the network. The graph first has to be modified in order to include neutral (1-weighted per edge) source and sink nodes

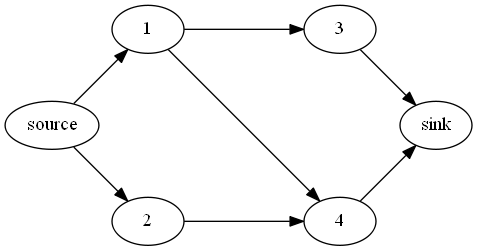
After this modification the same algorithm can be applied to obtain a maximum flow of 2 (i.e. two nodes of the left set are suitable to be associated with nodes of the right set).