Kth order statistic
Wikipedia defines the kth order statistic as
In statistics, the kth order statistic of a statistical sample is equal to its kth-smallest value.
A trivial way to find the kth order statistic is to simply sort an input vector and get the kth element. This approach takes \( O(n \log{n}) \).
A better approach exploits the fact that heaps can be constructed in linear time from an input array.
Efficient O(n) heapify
There are two ways to recursively construct a heap: siftDown or siftUp.
-
siftUp is the easiest one and just adds one element at a time to the heap and moves it up the tree to the right position (possibly till position 0 - the root). Since each insertion can require a maximum of \( \log{n} \) swaps, this approach for \( n \) elements takes \( O(n \log{n}) \).
-
siftDown is slightly more complicated but ensures better performances. It starts with a broken heap in array form and, since the last child of the heap at position
ihas its parent at indexp = i / 2, calling siftDown on indexprecursively until the heap property is verified grants a different complexity.
Suppose we have a binary tree of height \( h = 3 \). There are \( 2^{h-j} \) nodes at every level \( j \)
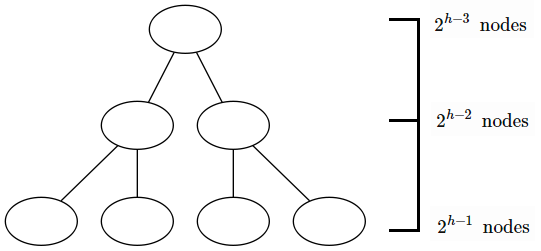
Since every node can descend up to \( j \) levels due to siftDown, we have that at each level \( j \) there are \( 2^{h-j} \) nodes that can descend \( j \) times
\[T(n) = \sum_{j=0}^{h}{j2^{h-j}} = \sum_{j=0}^{h}{j \frac{2^{h}}{2^{j}}} = 2^{h}\sum_{j=0}^{h}{ \frac{j}{2^{j}}}\]so the total time is equivalent to that sum. In order to solve the total time required, a few observations are necessary. The geometric series for any constant \( x < 1 \) is
\[\sum_{j=0}^\infty{x^j} = \frac{1}{1-x}\]Now if we take the derivative of this formula and multiply both sides by \( x \) we get
\[\sum_{j=0}^\infty{jx^{j-1}} = \frac{1}{(1-x)^2} \ \sum_{j=0}^\infty{jx^{j}} = \frac{x}{(1-x)^2}\]now by plugging \( x = 1/2 \) into this formula we get exactly the sum we were searching for
\[\sum_{j=0}^\infty{\frac{j}{2^j}} = 2\]We can use this result as an approximation since the sum is bounded to that value thus we get
\[T(n) = 2^{h}\sum_{j=0}^{h}{ \frac{j}{2^{j}}} \le 2^{h}\sum_{j=0}^{\infty}{ \frac{j}{2^{j}}} \le 2^h \cdot 2 = 2^{h+1}\]Since the number of nodes in the tree is \( 2^{h+1} - 1 \) we have \( T(n) \le n + 1 \in O(n) \).
Bottom line is: heapify by siftDown is faster. Also notice that since child with index \( i \) has parent \( p = i / 2 \), the siftDown recursion needs to be executed only from \( \text{array_size} / 2 \to 0 \).
void swimDownHeapify(vector<int>& heap, int index) {
int left = (index + 1) * 2 - 1;
int right = (index + 1) * 2 + 1 - 1;
int smallest = index;
if (left < heap.size() && heap[index] > heap[left])
smallest = left;
if (right < heap.size() && heap[smallest] > heap[right])
smallest = right;
if (smallest != index) {
swap(heap[index], heap[smallest]);
swimDownHeapify(heap, smallest);
}
}
vector<int> vec = { 6, 5, 3, 1, 8, 7, 2, }; // random data
vector<int> heap(vec);
for (int i = (heap.size() / 2) - 1; i >= 0; --i) {
swimDownHeapify(heap, i);
}Heap-powered kth order statistic
Exploiting this fact, the kth order statistic can be extracted by building a heap in \( O(n) \) and repeatedly extracting the minimum and reheapifying afterwards. This last process for a single element from the root is in the order of \( O(\log{n}) \) and thus the total time is \( O(n + k \log{n}) \)
#include <iostream>
#include <vector>
using namespace std;
void swimDownHeapify(vector<int>& heap, int index) {
int left = (index + 1) * 2 - 1;
int right = (index + 1) * 2 + 1 - 1;
int smallest = index;
if (left < heap.size() && heap[index] > heap[left])
smallest = left;
if (right < heap.size() && heap[smallest] > heap[right])
smallest = right;
if (smallest != index) {
swap(heap[index], heap[smallest]);
swimDownHeapify(heap, smallest);
}
}
int findKthOrderStatistic(vector<int>& vec, int k) {
if (k > vec.size() || k < 1)
return -1;
vector<int> heap(vec);
// Build the heap
for (int i = static_cast<int>((heap.size() / 2) - 1); i >= 0; --i) {
swimDownHeapify(heap, i);
}
// Extract the minimum k times
int kth = -1;
for (int i = 0; i < k; ++i) {
kth = heap[0];
// Reheapify
swap(heap[0], heap[heap.size() - 1]);
heap.resize(heap.size() - 1);
swimDownHeapify(heap, 0);
}
return kth;
}
int main() {
vector<int> vec = { 6, 5, 3, 1, 8, 7, 2 };
int k = 4;
cout << findKthOrderStatistic(vec, k); // 5
}Efficient linear-time Kth order statistic
One last method to get the kth order statistic proves to be even faster than the ones analyzed few paragraphs ago. The algorithm builds on quickselect and enhances it by improving its worst-case of \( O(n^2) \). A simple quickselect would look like the following
#include <iostream>
#include <vector>
using namespace std;
int partition(vector<int>& vec, int left, int right, int pivot) {
swap(vec[pivot], vec[left]); // No-op if pivot is the first one
pivot = left;
int i = left;
int j = right + 1;
while (i < j) {
while (++i < j && vec[i] < vec[pivot]);
while (--j >= i && vec[j] >= vec[pivot]); // Beware: tricky indices
if (i <= j)
swap(vec[i], vec[j]);
}
swap(vec[pivot], vec[j]);
return j;
}
int quickSelect(vector<int>& vec, int left, int right, int k) {
if (left == right)
return vec[left];
int pivot = left; // Just grab the first element as pivot
int mid = partition(vec, left, right, pivot);
if (k - 1 == mid)
return vec[mid];
if (k - 1 < mid)
return quickSelect(vec, left, mid - 1, k);
else
return quickSelect(vec, mid + 1, right, k);
}
int findKthOrderStatistic(vector<int>& vec, int k) {
return quickSelect(vec, 0, static_cast<int>(vec.size() - 1), k);
}
int main() {
vector<int> vec = { 6, 5, 3, 1, 8, 7, 2 };
int k = 4;
cout << findKthOrderStatistic(vec, k); // 5
return 0;
}The critical point of the algorithm regards the choice of the pivot element. A bad pivot element would increase running time while a good pivot element (i.e. one that evenly divides the elements) would reduce it.
The median of medians variant of the above algorithm exploits finding an approximate median of the elements in linear time to gain a good pivot point from where to start partitioning.
The pseudocode of the algorithm is roughly as follows
quickSelect(vector, k)
subgroups = divide vector into subgroups of 5 elements each
medians = for every subgroup find its median
// Grab the median of medians
medianOfMedians = quickSelect(medians, medians.size() / 2)
int mid = partition(vector, medianOfMedians)
if mid is k
return vector[mid]
if k is less than mid
return quickSelect(lower_half(vector), k)
else
return quickSelect(upper_half(vector), k)
Since finding the median of each subgroup of 5 elements is \( O(n) \) and partitioning also takes \( O(n) \), the interesting analysis takes place in the recursive steps. The question to ask is: what is the maximum number of elements which can be greater or less than the medianOfMedians?
Let’s focus on the maximum number of elements which are greater than it: approximately half of the \( \lceil \frac{n}{5} \rceil \) groups have a median greater than medianOfMedians; that means, since we have 5 elements groups, each one of them contributed with 3 elements greater than medianOfMedians. Thus we have
\[3 \Bigg (\Bigg \lceil \frac{1}{2} \bigg \lceil \frac{n}{5} \bigg \rceil \Bigg \rceil \Bigg) - lg \ge \frac{3n}{10} - lg\]where \( lg \) indicates the number of elements of a less-than-5-elements group. In the worst case the function recurs for \( n - (\frac{3n}{10} - lg) \). This quantity is an upper-bound if the number of elements is greater than a constant \( c \) so
\[T(n) \le T(\frac{n}{5}) + T(\frac{7n}{10}) + O(n) \ if \ n \ge c\]therefore the runtime is \( O(n) \) in the worst case. Complete code follows.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int partition(vector<int>& vec, int left, int right, int pivot) {
swap(vec[pivot], vec[left]); // No-op if pivot is the first one
pivot = left;
int i = left;
int j = right + 1;
while (i < j) {
while (++i < j && vec[i] < vec[pivot]);
while (--j >= i && vec[j] >= vec[pivot]); // Beware: tricky indices
if (i <= j)
swap(vec[i], vec[j]);
}
swap(vec[pivot], vec[j]);
return j;
}
int quickSelect(vector<int>& vec, int left, int right, int k) {
if (left == right)
return vec[left];
// Calculate the median of medians and return its index in the original vector
const int N = right - left + 1;
auto findMedian = [](vector<int>& subgroup) {
sort(subgroup.begin(), subgroup.end());
return subgroup[subgroup.size() / 2];
};
vector<int> medians;
for (int i = 0; i < (N + 4) / 5; ++i) {
int elements = 5;
if (i * 5 + 5 > N)
elements = N % 5;
vector<int> subgroup;
for (auto it = vec.begin() + left + i * 5;
it != vec.begin() + left + i * 5 + elements; ++it)
subgroup.emplace_back(*it);
medians.push_back(findMedian(subgroup));
}
// Now find the median of medians via quickselect
int medianOfMedians = (medians.size() == 1) ? medians[0] :
quickSelect(medians, 0, static_cast<int>(medians.size() - 1),
static_cast<int>(medians.size() / 2));
// Find its original index
int medianOfMediansIndex;
for (int i = 0; i < vec.size(); ++i) {
if (vec[i] == medianOfMedians) {
medianOfMediansIndex = static_cast<int>(i);
break;
}
}
int pivot = medianOfMediansIndex; // Use it as a pivot
int mid = partition(vec, left, right, pivot);
if (k - 1 == mid)
return vec[mid];
if (k - 1 < mid)
return quickSelect(vec, left, mid - 1, k);
else
return quickSelect(vec, mid + 1, right, k);
}
int findKthOrderStatistic(vector<int>& vec, int k) {
return quickSelect(vec, 0, static_cast<int>(vec.size() - 1), k);
}
int main() {
vector<int> vec = { 6, 5, 3, 1, 8, 7, 2 };
int k = 4;
cout << findKthOrderStatistic(vec, k); // 5
return 0;
}