Implementing arithmetic operations using bit operations is usually a common interview question although its practical use is arguably quite limited. Most platforms support basic arithmetic operations and the only cases where arithmetic at binary level could be useful are circuits design (half-adders, subtractors and that sort of circuitry).

Nonetheless it could be a useful thought exercise. Most of the considerations in this article assume a 2’s complement machine but the algorithms can also be ported to different architectures using a different number representation.

Addition

Implementing addition builds on the same logic of a half-adder

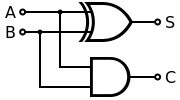
The key concept is to split the sum and the carry into two channels. Let’s take the binary representation of 2 and 1: 10 and 1. Adding these together would not require any carry and therefore it can be accomplished with a simple xor

If a carry is necessary as in 3 + 1, anding the binary representations and shifting left of one place would yield exactly a number containing the carries

At this point we can xor again the carry and the sum in order to obtain another sum and (possibly) another carry. This approach mimics the addition we were used to do on paper in primary school.

int addition(int x, int y) {
  if (y == 0)
    return x;
  else
    return addition(x ^ y, (x & y) << 1);
}

The recursion stops when there’s no carry to bring forward.

Subtraction

Subtraction works in a similar way with a difference: there are no carries but borrows.

The sum part with the xor seems a bit counter-intuitive for a subtraction, but once a borrow is performed (and later subtracted via another xor) the result is exactly a binary addition. The borrows are obtained by detecting the

situations, i.e. where the subtrahend is greater than the minuend (and thus a borrow is required): \( \neg x \oplus y \)

int subtraction(int x, int y) {
  if (y == 0)
    return x;
  else
    return subtraction(x ^ y, (~x & y) << 1);
}

in a 2’s complement representation the above operations also work for negative numbers.

Multiplication

Multiplication builds on the addition explained above. Implementing a multiplication \( x \cdot y \) by just adding \( y \) times \( x \) works but it’s quite slow. A better approach would be again to just mimic the long multiplication we learned in primary school in binary

if the rightmost value of y is 1
  add the entire x to result

shift x left by one position
shift y right by one position

int multiplication(int x, int y) {
  int result = 0;

  while (y != 0) {

    if (y & 0x1)
      result = result + x;

    x <<= 1;
    y >>= 1;
  }

  return result;
}

Division

The same holds for the division: a long division approach (although quite tedious to implement) is one of the best choices.

int division(int x, int y) {
  // Handle particular cases
  if (x < y)
    return 0;
  if (x == y)
    return 1;
  if (y == 0)
    throw std::logic_error("Division by zero"); // Handle this somehow

  int result = 0;
  int position = 1;
  while (x > y) {
    y <<= 1;
    position <<= 1;
  }

  y >>= 1;
  position >>= 1;
  while (position != 0) {

    if (x > y) {
      result |= position;
      x -= y;
    }

    y >>= 1;
    position >>= 1;
  }

  return result;
}

We will now complement this post with other non-strictly bit operation based approaches to build upon the operations we’ve seen to avoid common library functions.

Exponentiation

Calculating the n-th power of a number can also be efficiently done with a fast technique called exponentiation by squaring.

The basic concept relies on the following recursion

A recursive approach naturally follows

int pow(int x, int y) {
  if (y == 0)
    return 1;
  else
    return pow(x*x, y >> 1) * ((y % 2 != 0) ? x : 1);
}

The same iterative version might be more readable though

int pow(int x, int y) {

  int result = 1;
  while (y != 0) {

    if (y % 2 != 0)
      result *= x;

    x *= x;
    y >>= 1;
  }

  return result;
}

Regarding the fact that we used the modulo operator to get the remainder in the snippets above, this can be implemented in several trivial ways, e.g. by just looping over the divisor until it is greater than the dividend and returning their difference and keeping in mind

as particular cases if negative integer support needs to be implemented.

Square root

The solution builds upon a simpified case of Newton’s Method. Newton’s method builds on the tangent equation of a first-guess point for a function

by setting \( y = 0 \) and using the \( x \) coordinate as the next input, we obtain the recursive relation

and since we’re searching for the point for which \( f(x) = x^2 - S = 0 \), we have

This last recursion is the so-called Babylonian method which basically consists of a first-time approximation for \( x \) (the closer to the real square root, the faster the convergence) and of a recursive relation which ends when we’re satisfied with the error range (i.e. we’re operating in a sufficiently small interval)

#include <iostream>
using namespace std;

float squareRoot(float n) {
  float x = n;
  float y = 1; // S / x == n / n
  float e = 0.00001f; // Accuracy level
  while (x - y > e) {
    x = (x + y) / 2;
    y = n / x;
  }
  return x;
}

int main() {
  int n = 50;
  float sq = squareRoot(static_cast<float>(n));
  cout << "Approximate square root of " << n << " is " << sq;
}