Gray code subsets generation
A gray code is a binary numeral system where two successive items differ in only one bit. Gray code sequences have many applications ranging from error correction to genetic algorithms mutations due to their hamming distance properties.
A non-binary system can also be used to generate all subsets of a set of items. Let’s take for instance the set \( S = { 1,2,3} \)
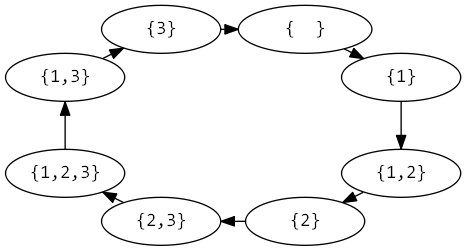
The given code computes the gray code sequence representing all \( 2^N \) possible subsets of the given input sequence
#include <iostream>
#include <iterator>
#include <vector>
using namespace std;
int main() {
vector<int> v = { 1, 2, 3 };
vector<vector<int>> gcodes(1); // Empty set
for (int i = 0; i < static_cast<int>(v.size()); ++i) {
vector<vector<int>> newElements;
for (decltype(gcodes)::reverse_iterator it = gcodes.rbegin();
it != gcodes.rend(); ++it) {
newElements.push_back(*it);
newElements.back().push_back(v[i]);
}
gcodes.insert(gcodes.end(), newElements.begin(), newElements.end());
}
// Print out the gray code
cout << "Gray codes for the input set: " << endl;
for (auto& v : gcodes) {
cout << "{ ";
copy(v.begin(), v.end(), ostream_iterator<int>(cout, " "));
cout << "}" << endl;
}
return 0;
}For the set of three elements above the algorithm performs a total of \( 2^0 + 2^1 + 2^2 \) operations to insert new elements from the previous ones. This yields a \( O(2^{N-1}) \) complexity.