This problem appeared in a SO question asking for help converting a recursive \( O(N^k) \) solution into a bottom-up dynamic programming one \( O(kN^2) \) where k is the number of allowed steps and N is the number of nodes in a graph.

As noted on the post given a sample graph

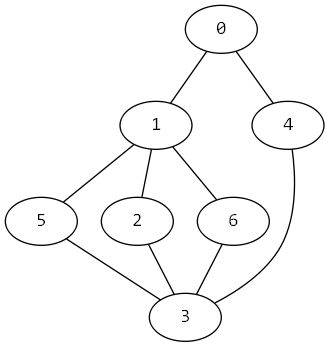
graph

and setting \( k = 5 \) yields a total of 6 possible roundtrip paths from the origin node

0-1-2-3-4-0
0-1-5-3-4-0
0-1-6-3-4-0
0-4-3-6-1-0
0-4-3-5-1-0
0-4-3-2-1-0

The code to solve the problem is posted in the answer I gave, anyway I’ll repost it for convenience

/**
* Count the number of ways we can go from station 0 to station destination
* traversing exactly nSteps edges with dynamic programming. The algorithm
* runs in O(k*N^2) where k is the number of tickets and N the number of
* stations.
*/
unsigned int tripCounter(const Subway& subway, int destination, int nSteps)
{
  map<int, vector<int>> m;
  for (int i = 0; i < nSteps + 1; ++i)
    m[i].resize(subway.nStations, 0);

  m[0][0] = 1; // Base case

  for (int t = 1; t < m.size(); ++t) { // For each ticket

    vector<int> reachedStations;
    for (int s = 0; s < subway.nStations; ++s) { // For each station
      if (m[t-1][s] > 0)
        reachedStations.push_back(s); // Store if it was reached in the previous state
    }

    for (auto s : reachedStations) {
      // Find adjacent stations
      for (int adj = 0; adj < subway.nStations; ++adj) {
        if (s == adj)
          continue;
        if (subway.connected[s][adj])
          m[t][adj] += m[t-1][s];
      }
    }
  }
  return m[nSteps][0];
}

The algorithm assumes an adjacency matrix to store the subway graph.