Bitonic tour

In computational geometry the bitonic tour of a set of points is a closed polygonal chain formed by all the vertices in the set and that has the property of intersecting at most twice with any vertical line.

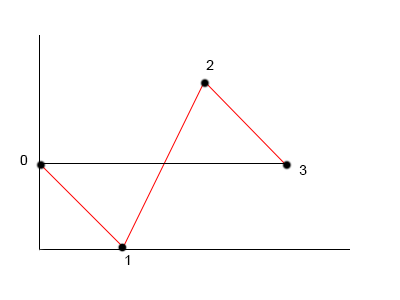
An example trace

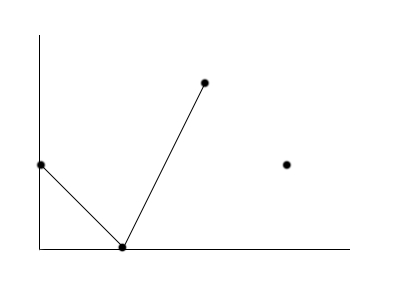
As an example the following is not a bitonic tour

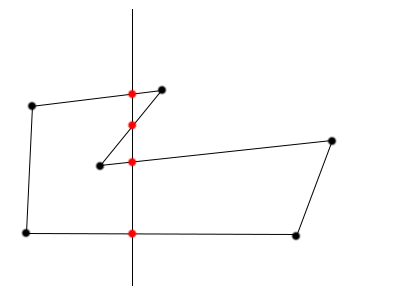
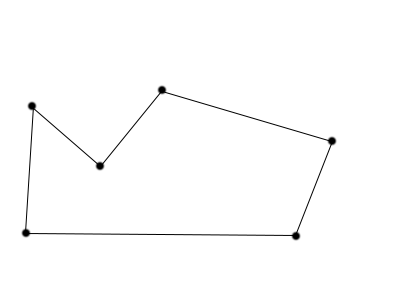
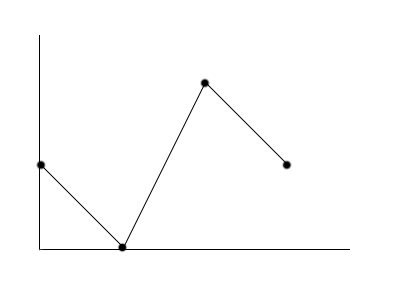
while the following is

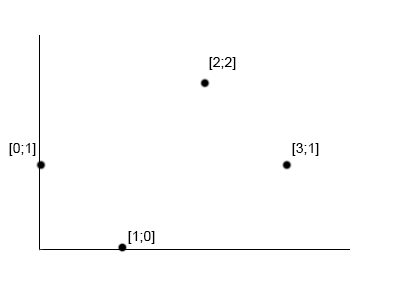
It is defined as the optimal bitonic tour the minimum-length path which forms a bitonic tour. The best bitonic tour also minimizes the horizontal motion while covering all of the vertices in the set. Let us consider for instance the following set of points in a 2D Cartesian coordinates space

{0, 1}
{1, 0}
{2, 2}
{3, 1}

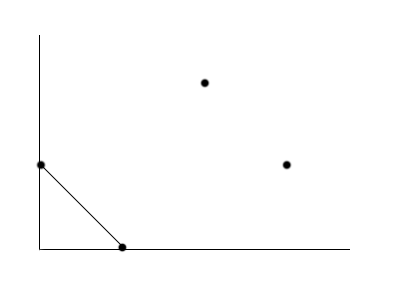
By ordering the points according to their \( x \) value in increasing order and recursively adding the euclidean distance of a new point in the sequence from the starting point 0 we obtain the first bitonic paths. Let us denote with bitonicDistances[x][y] the clockwise bitonic path starting from x and ending in y

bitonicDistances[0][0] = 0

bitonicDistances[0][1] = bitonicDistances(0,0) + euclideanDistance(0,1)

bitonicDistances[0][2] = bitonicDistances(0,1) + euclideanDistance(1,2)

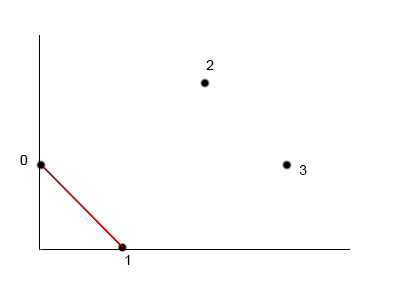
bitonicDistances[0][3] = bitonicDistances(0,2) + euclideanDistance(2,3)

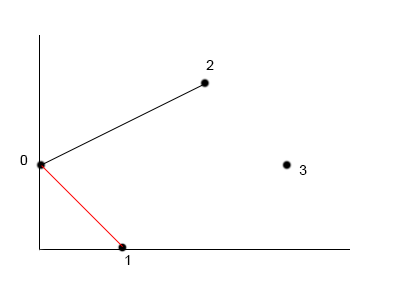
We can now iteratively try to set each point as the starting x and move the end point by one at each substep. In the graphs below the red line denotes the bitonic path that links x to an intermediate point less than x (e.g. bitonicDistances(0,1) where the intermediate point is 0 since bitonicDistances(0,1) = bitonicDistances(1,0)) and the black line denotes the euclidean distance to complete the path requested

bitonicDistances[1][1] = bitonicDistances(0,1) + euclideanDistance(0,1)

bitonicDistances[1][2] = bitonicDistances(0,1) + euclideanDistance(0,2)

bitonicDistances[1][3] = bitonicDistances(1,2) + euclideanDistance(2,3)

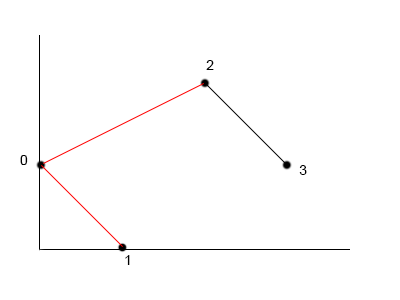
To calculate the bitonic distance that starts from point 2, makes a clockwise path including all the previous points to 0 and from 0 starts again clockwise and returns to the end 2, we need to take into account two possible choices:

1. The path starts from 2, goes to 0 and returns to 2
2. The path starts from 2, goes to 1 and returns to 2

This is the key of the recursive approach we’re following: evaluating different bitonic paths to find the minimum cost one as the final bitonic tour from a start point to and end point

bitonicDistances[2][2] = min between {
  bitonicDistances(0,2) + euclideanDistance(0,2)
  bitonicDistances(1,2) + euclideanDistance(1,2)
}

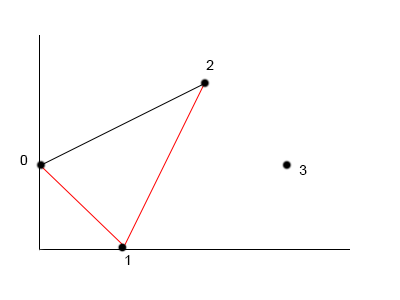
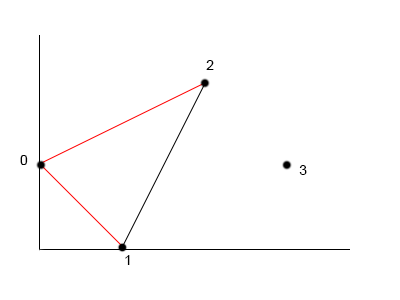
It has to be noted that in the case above the two bitonic paths are of the same length and therefore any could be chosen.

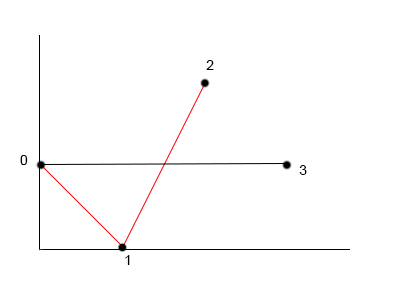
bitonicDistances[2][3] = min between {
  bitonicDistances(0,2) + euclideanDistance(0,3)
  bitonicDistances(1,2) + euclideanDistance(1,3) (best choice)
}

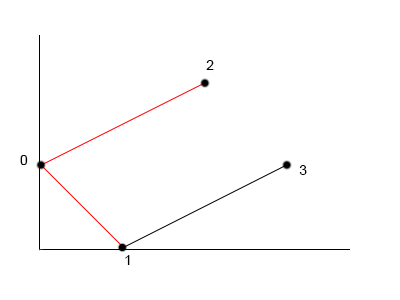
bitonicDistances[3][3] = min between {
  bitonicDistances(0,3) + euclideanDistance(0,3)
  bitonicDistances(1,3) + euclideanDistance(1,3) (best choice)
  bitonicDistances(2,3) + euclideanDistance(2,3) (best choice)
}

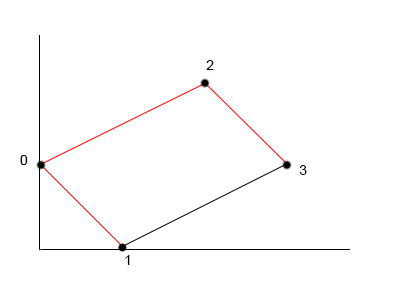
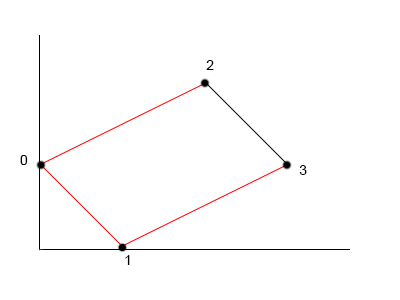
Therefore one of the two final bitonic best paths is chosen as candidate for the best bitonic tour of length 7.30056.

Dynamic programming

The approach described above is well suited to being implemented with a dynamic programming approach. Let \( BD(i,j) \) be bitonicDistances variable described above, i.e. the minimum cost bitonic path from \( i \) to \( j \). It follows that

The code for this recursion follows

#include <iostream> 
#include <vector>
#include <algorithm>
using namespace std;

struct Point {
  float x;
  float y;
};

float bitonicTourCost(vector<Point> points) {
  const size_t N = points.size();

  // Sort the points by increasing x coordinates

  sort(points.begin(), points.end(), [](const Point& a, const Point& b) {
    if (a.x < b.x)
      return true;
    else
      return false;
  });

  auto euclideanDistance = [&](int a, int b) {
    return sqrt(pow(points[a].x - points[b].x, 2) + 
                pow(points[a].y - points[b].y, 2));
  };

  // Adjacency matrix for bitonic distances between points

  vector<vector<float>> bitonicDistances(N, vector<float>(N, -1));
  bitonicDistances[0][0] = 0;
  for (int i = 1; i < N; ++i)
    bitonicDistances[0][i] = 
                      bitonicDistances[0][i-1] + euclideanDistance(i - 1, i);

  for (int i = 1; i < N; ++i) {
    for (int j = i; j < N; ++j) {
      float minimum = numeric_limits<float>::max();
      if (i == j || i == j - 1) {
        for (int k = 0; k < i; ++k) {
          float opt = bitonicDistances[k][i] + euclideanDistance(k, j);
          minimum = min(minimum, opt);
        }
        bitonicDistances[i][j] = minimum;
      } else {
        bitonicDistances[i][j] = 
                      bitonicDistances[i][j - 1] + euclideanDistance(j - 1, j);
      }
    }
  }

  return bitonicDistances[N - 1][N - 1];
}


int main() {

  vector<Point> points = {
    {0, 1},
    {1, 0},
    {2, 2},
    {3, 1}
  };

  cout << bitonicTourCost(points);
  
  return 0; 
}

The algorithm runs in \( O(N^2) \).