Tree traversal is one of the most common operations and one of the easiest to implement by recursion on a binary tree data structure. Implementing a recursive pre-order, in-order and post-order traversal is absolutely straightforward

struct Node {
  Node(int val) : value(val) {}
  Node(int val, Node *l, Node *r) : value(val) {
    left.reset(l);
    right.reset(r);
  }
  int value;
  unique_ptr<Node> left, right;
};

void recursivePreOrderPrint(const unique_ptr<Node>& node) {
  if (!node)
    return;
  cout << " " << node->value << " ";
  recursivePreOrderPrint(node->left);
  recursivePreOrderPrint(node->right);
}

void recursiveInOrderPrint(const unique_ptr<Node>& node) {
  if (!node)
    return;
  recursiveInOrderPrint(node->left);
  cout << " " << node->value << " ";
  recursiveInOrderPrint(node->right);
}

void recursivePostOrderPrint(const unique_ptr<Node>& node) {
  if (!node)
    return;
  recursivePostOrderPrint(node->left);
  recursivePostOrderPrint(node->right);
  cout << " " << node->value << " ";
}

Implementing pre-order, in-order and post-order iteratively proves to be slightly harder. By using a stack it is possible to implement all three of them with relatively few lines of code. Pseudocode and code follow

Pre-order
  push root node
  while stack is not empty
    print node
    pop it
    push right and left children

In-order
  push root node
  while there's a left node
    push left node
    node = left node
  while stack is not empty
    print node
    pop it
    if there's a right node
      push right node
      while there's a left node
        push left node
        node = left node

Post-order
  root = pointer to root node
  while root is not null
    push right node
    push root
    root = root.left
  while stack is not empty
    if there is no right node
      print it
      pop it
    else
      if the right node is on the stack below me
        exchange first node with second node in the stack
        root = first node (i.e. former right child)
        while root is not null
          push right node
          push root
          root = root.left
      else
        print it
        pop it

void iterativePreOrderPrint(const unique_ptr<Node>& node) {
  stack<const Node*> st;
  st.push(node.get());
  while (!st.empty()) {
    const Node* top = st.top();
    cout << " " << top->value << " ";
    st.pop();
    if (top->right)
      st.push(top->right.get());
    if (top->left)
      st.push(top->left.get());
  }
}

void iterativeInOrderPrint(const unique_ptr<Node>& node) {
  stack<const Node*> st;
  st.push(node.get());
  while (st.top()->left)
    st.push(st.top()->left.get());
  while (!st.empty()) {
    const Node* top = st.top();
    cout << " " << top->value << " ";
    st.pop();
    if (top->right) {
      st.push(top->right.get());
      while (st.top()->left)
        st.push(st.top()->left.get());
    }
  }
}

void iterativePostOrderPrint(const unique_ptr<Node>& node) {
  stack<const Node*> st;
  const Node *root = node.get();
  while (root != nullptr) {
    if (root->right)
      st.push(root->right.get());
    st.push(root);
    root = (root->left) ? root->left.get() : nullptr;
  }
  while (!st.empty()) {
    const Node* top = st.top();
    if (top->right && st.size() > 1) {
      // Due to the restrictness of std::stack adaptor this code peeks

      // into the 2nd top element by doing multiple pops/pushes

      st.pop();
      const Node *second = st.top();
      st.pop();
      if (top->right.get() == second) {
        st.push(top);
        root = second;
        while (root != nullptr) {
          if (root->right)
            st.push(root->right.get());
          st.push(root);
          root = root->left.get();
        }
      }
      else {
        st.push(second);
        cout << " " << top->value << " ";
      }
    }
    else {
      cout << " " << top->value << " ";
      st.pop();
    }
  }
}

In-Order Morris traversal

Another \( O(n) \) method of implementing a non-recursive in-order traversal without even using a stack is due to the Morris Traversal algorithm which builds on threaded binary trees by agumenting predecessor nodes with right links to their successors in the first phase and removes these links in the second phase. E.g. given the tree

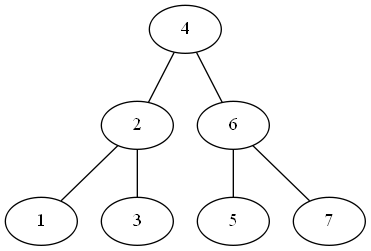
the algorithm starts from the root and if there’s a left node tries to find the rightmost predecessor of the current node. When it is found, since it features a nullptr as right child, this pointer is temporarily modified to point to the current node (i.e. its successor)

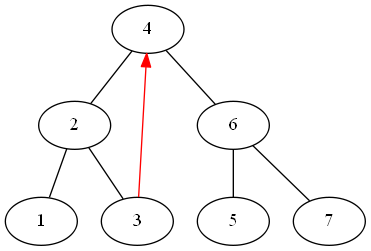
it then proceeds doing the same until a leftmost node with no left child is found

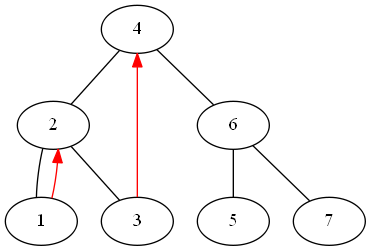
at this point the second phase starts: the node with no left child is printed out (1 in the example) and the right pointer is used to get to the successor node 2. The algorithm would proceed in the same way as phase 1 by finding again 2’s predecessor, but this time the predecessor has no nullptr as right child since it was augmented before. Therefore the predecessor was already printed and processed: the current node is printed and the graph restored by deleting the predecessor’s right link and advancing to the next right value (successor)

void MorrisTraversalInOrderPrint(unique_ptr<Node>& node) {
  Node *current = node.get();
  while (current != nullptr) {
    if (current->left) {
      Node *predecessor = current->left.get();

      // Find predecessor of current but stop if it was already augmented

      while (predecessor->right && predecessor->right.get() != current)
        predecessor = predecessor->right.get();

      if (predecessor->right == false) {
        predecessor->right.reset(current);
        current = current->left.get();
      } else {
        // Restore the tree

        predecessor->right.release();
        cout << " " << current->value << " ";
        current = current->right.get();
      }
    }
    else {
      cout << " " << current->value << " ";
      current = current->right.get();
    }
  }
}

References

Morris Traversal