All pairs shortest path and transitive closure

The all pairs shortest path problem is a classic one involving finding the shortest path between all vertices. The idea is to be able to perform the query for the shortest path distance between \( i \) and \( j \) in \( O(1) \). A simple dynamic programming algorithm is the Floyd–Warshall algorithm which doesn’t work for negative weighted cycles.

Given the following graph

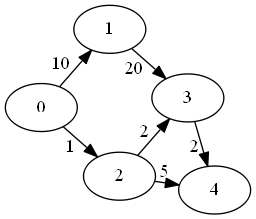
the following dynamic programming algorithm computes the all-pairs-shortest-path distance matrix

#include <iostream>
#include <vector>
#include <iterator>
using namespace std;

vector<vector<int>> allPairsShortestPath(const vector<vector<int>>& adjMatrix) {
  // Assumes adjMatrix hasn't null dimensions
  vector<vector<int>> result(adjMatrix);
  
  // Consider each vertex as an intermediate vertex in a path
  for (int k = 0; k < adjMatrix.size(); ++k) {
    // Form all possible paths
    for (int i = 0; i < adjMatrix.size(); ++i) {
      for (int j = 0; j < adjMatrix.size(); ++j) {
        if (result[i][k] + result[k][j] < result[i][j])
          result[i][j] = result[i][k] + result[k][j];
      }
    }
  }
  return result;
}

int main() {
  const int INF = 10000; // Caveat: this should be chosen not to overflow
  vector<vector<int>> adjMatrix = {
    { 0,   10,  1,   INF, INF },
    { INF, 0,   INF, 20,  INF },
    { INF, INF, 0,   2,   5 },
    { INF, INF, INF, 0,   2 },
    { INF, INF, INF, INF, 0 }
  };

  auto result = allPairsShortestPath(adjMatrix);

  cout << "All pairs shortest path matrix:" << endl;
  for (auto& v : result) {
    copy(v.begin(), v.end(), ostream_iterator<int>(cout, "\t"));
    cout << endl;
  }

  return 0;
}

Output

All pairs shortest path matrix:
     10      1       3       5
 0       10000   20      22
 10000   0       2       4
 10000   10000   0       2
 10000   10000   10000   0

As it can easily be guessed, the algorithm isn’t particularly efficient and is \( O(N^3) \). There are other faster algorithms for the all-pairs-shortest-path problem but Floyd-Warshall’s is an elegant example of dynamic programming solution that can also be used for the transitive closure problem in graph theory. It is trivial to modify the algorithm above to answer the question Is it possible to get from node x to y in one or more steps?