A common distortion which might occur when dealing with computer vision tasks involving wide-angle cameras is barrel distortion caused by a greater magnification at the center of the lens compared than the one at the edges.

Zhang, 1999 showed that the polynomial radial distortion model with two coefficients can be modeled as

\[r_d = r(1+k_1 r^2 + k_2 r^4)\]

we might consider a simpler approximation of this model for radial distortion Fitzgibbon, 2001

\[r_d = r_u(1 - \alpha |r_u|^2) \leftrightarrow r_u = \frac{r_d}{1 - \alpha {r_d}^2}\]

where \( r_u \) and \( r_d \) are the distances from the center of distortion in the undistorted and distorted images. \( \alpha \) is a constant specific to the lens type used.

In order to actually implement such an approximation a mapping between the original coordinates of a point in the image and the coordinates in a normalized \( [-1;+1] \) coordinate system is needed

\[x_n = (2x - w) / w \\ y_n = (2y - h) / h\]

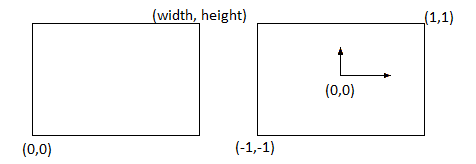
(\( (x_n,y_n) \) stands for the normalized coordinates, \( w,h \) for width and height) and their inverse counterparts

\[x = \frac{(x_n + 1) * w}{2} \\ y = \frac{(y_n + 1) * h}{2}\]

Implementing with OpenGL shaders

Given a simple textured quad which gets mapped to a radial distorted image, the filtering could be efficiently performed in the fragment shader

precision mediump float;

uniform sampler2D texture_diffuse;
uniform vec2 image_dimensions;
uniform float alphax;
uniform float alphay;

varying vec4 pass_Color;
varying vec2 pass_TextureCoord;

void main(void) {

  // Normalize the u,v coordinates in the range [-1;+1]

  float x = (2.0 * pass_TextureCoord.x - 1.0) / 1.0;
  float y = (2.0 * pass_TextureCoord.y - 1.0) / 1.0;
  
  // Calculate l2 norm

  float r = x*x + y*y;
  
  // Calculate the deflated or inflated new coordinate (reverse transform)

  float x3 = x / (1.0 - alphax * r);
  float y3 = y / (1.0 - alphay * r); 
  float x2 = x / (1.0 - alphax * (x3 * x3 + y3 * y3));
  float y2 = y / (1.0 - alphay * (x3 * x3 + y3 * y3));	
  
  // Forward transform

  // float x2 = x * (1.0 - alphax * r);

  // float y2 = y * (1.0 - alphay * r);


  // De-normalize to the original range

  float i2 = (x2 + 1.0) * 1.0 / 2.0;
  float j2 = (y2 + 1.0) * 1.0 / 2.0;

  if(i2 >= 0.0 && i2 <= 1.0 && j2 >= 0.0 && j2 <= 1.0)
    gl_FragColor = texture2D(texture_diffuse, vec2(i2, j2));
  else
    gl_FragColor = vec4(0.0, 0.0, 0.0, 1.0);
}

A sample WebGL implementation follows

References

  • Zhang Z. (1999). Flexible camera calibration by viewing a plane from unknown orientation

  • Andrew W. Fitzgibbon (2001). Simultaneous linear estimation of multiple view geometry and lens distortion