The problem can be expressed as follows: given two line segments \( {p_1,p_2} \) and \( {p_3,p_4} \) check if they intersect with each other.

Before discussing a possible solution a concept has to be introduced: orientation.

Orientation

The orientation of an ordered triplet of points \( {p_1,p_2,q_1} \) in the plane can be defined as

  • Clockwise

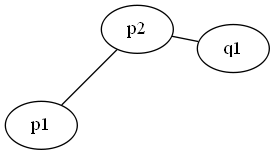
image

  • Counterclockwise

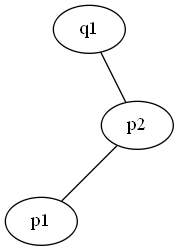
image

  • Collinear

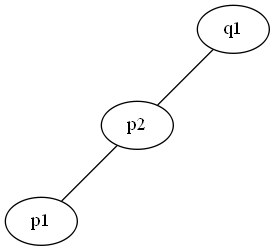
image

Orientation plays a crucial role in the intersection test. Let the slopes of the segments be respectively \( \sigma,\tau \)

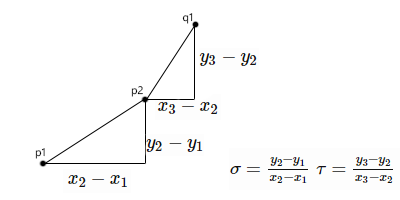
image

the orientation test should return

  • Counterclockwise if \( \sigma < \tau \)
  • Clockwise if \( \sigma > \tau \)
  • Collinear if \( \sigma = \tau \)

The orientation therefore depends on the expression

\[(y_2 - y_1)(x_3 - x_2) - (y_3 - y_2)(x_2 - x_1)\]

yielding a positive, zero or negative result. In code

int orientation(const Point& p1, const Point& p2, const Point& q1) {
  int val = (p2.y - p1.y) * (q1.x - p2.x) - (q1.y - p2.y) * (p2.x - p1.x);
  if (val == 0)
    return 0;
  else
    return (val < 0) ? -1 : 1;
}

Intersection test

Two segments \( {p_1,p_2} \) and \( {q_1,q_2} \) intersect \( \iff \) one of the following conditions is verified

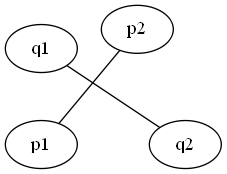
  1. General case

    \( {p_1,p_2,q_1} \) and \( {p_1,p_2,q_2} \) have different orientations and \( {q_1,q_2,p_1} \) and \( {q_1,q_2,p_2} \) have different orientations

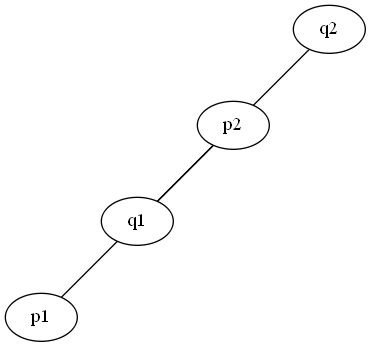
    image

  2. Special case

    All the points are collinear and either \( q_1 \) lies between \( p_1 \) and \( p_2 \) or \( q_2 \) lies between \( p_1 \) and \( p_2 \) (by checking the x-projections and y-projections).

    image

The code for intersection testing follows

#include <iostream>
#include <string>
#include <algorithm>
using namespace std;

struct Point {
  int x, y;
};

ostream& operator<<(ostream& os, const Point& p) {
  os << "{" << p.x << ";" << p.y << "}";
  return os;
}

int orientation(const Point& p1, const Point& p2, const Point& q1) {
  int val = (p2.y - p1.y) * (q1.x - p2.x) - (q1.y - p2.y) * (p2.x - p1.x);
  if (val == 0)
    return 0;
  else
    return (val < 0) ? -1 : 1;
}

// Returns true if q lies on p1-p2
bool onSegment(const Point& p1, const Point& p2, const Point& q) {
  if (min(p1.x, p2.x) <= q.x && q.x <= max(p1.x, p2.x) 
      && min(p1.y, p2.y) <= q.y && q.y <= max(p1.y, p2.y))
    return true;
  else
    return false;
}

bool intersectionTest(const Point& p1, const Point& p2,
  const Point& p3, const Point& p4) {
  int o1 = orientation(p1, p2, p3);
  int o2 = orientation(p1, p2, p4);
  int o3 = orientation(p3, p4, p1);
  int o4 = orientation(p3, p4, p2);

  // General case
  if (o1 != o2 && o3 != o4)
    return true;

  // Special cases
  if (o1 == 0 && onSegment(p1, p2, p3))
    return true;
  if (o2 == 0 && onSegment(p1, p2, p4))
    return true;
  if (o3 == 0 && onSegment(p3, p4, p1))
    return true;
  if (o4 == 0 && onSegment(p3, p4, p2))
    return true;

  return false;
}

int main() {

  auto printIntersection = [](auto p1, auto p2, auto p3, auto p4) {
    cout << boolalpha << "Intersection between segment " << p1 << " - "
      << p2 << " and segment " << p3 << " - " << p4 << ": " <<
      intersectionTest(p1, p2, p3, p4) << endl;
  };

  Point p1{ 0, 0 }, p2{ 5, 2 }, p3{ 0, 2 }, p4{ 7, 0 };

  printIntersection(p1, p2, p3, p4);

  p1 = { 0, 0 }, p2 = { 2, 2 }, p3 = { 1, 1 }, p4 = { 7, 1 };

  printIntersection(p1, p2, p3, p4);

  p1 = { 0, 0 }, p2 = { 2, 2 }, p3 = { 1, 0 }, p4 = { 3, 2 };

  printIntersection(p1, p2, p3, p4);

  p1 = { 0, 0 }, p2 = { 2, 2 }, p3 = { 1, 1 }, p4 = { 4, 4 };

  printIntersection(p1, p2, p3, p4);

  return 0;
}

References