The knapsack problem is a common combinatorial optimization problem: given a set of items \( S = {1,…,n} \) where each item \( i \) has a size \( s_i \) and value \( v_i \) and a knapsack capacity \( C \), find the subset \( S^{\prime} \subset S \) such that

A less mathematical but more intuitive explanation:

Imagine a burglar robbing a house with a sack of limited capacity: he must choose the items to steal in order to maximize his profit.

It has to be noted that a greedy algorithm would not work for most of the cases of the general problem. Take for instance the following algorithm

#include <iostream>
#include <vector>
#include <queue>
#include <functional>
using namespace std;

struct Item {
  int size;
  int value;
};

class ItemComparator {
public:
  // Swap if a.value < b.value (max priority queue)
  bool operator()(const Item& a, const Item& b) {
    return a.value < b.value;
  }
};

int main() {
  vector<Item> items = {
    {1, 4},
    {2, 5},
    {1, 2},
    {3, 6}
  };
  // A max heap queue
  priority_queue<Item, vector<Item>, ItemComparator> pq(items.begin(), items.end());
  const int C = 4;

  int currentCapacity = 0;
  int currentValue = 0;
  while (currentCapacity < C) {

    Item item{ -1, -1 };
    while (pq.empty() == false) {

      item = pq.top();
      pq.pop();

      if (currentCapacity + item.size <= C) // Try to fill with the maximum, otherwise
        break;                              // keep on searching for a smaller maximum
    }

    if (item.value == -1) // Could not find an element. Capacity exhausted
      break;

    currentCapacity += item.size;
    currentValue += item.value;
  }

  cout << "Reached a maximum of " << currentValue << "-worth objects and used "
       << currentCapacity << "/" << C << " capacity"; // 10-worth objects, 4/4
}

The algorithm uses a priority queue to maximize the profit each time abiding by the sack’s capacity. If an item cannot be picked up (no capacity left to store it), then the second-most-valuable item is picked and the test is repeated until there are no more items to steal that fits the remaining capacity.

The particular instance of the problem above fails to be optimally solved by the greedy approach:

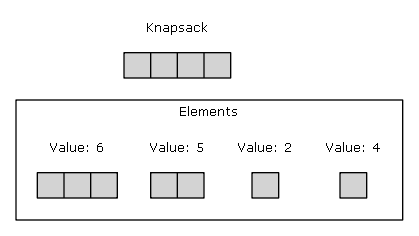
A human could realize in this simple instance that the greedy algorithm above doesn’t yield the optimal result since it first grabs the maximum value item 6 that, unfortunately, is also the bulkiest. Then grabs the second-maximum value 5, realizes it can’t be stored due to capacity constraints and grabs the third-maximum value 4.

Grand-total: element with value 6 and element with value 4 = 10.

The best solution is instead composed by all the elements except the biggest one: {element with value 5, element with value 2 and element with value 4} for a grand-total of 11.

Knapsack 0/1

The most common formulation of the knapsack problem is called 0/1 knapsack problem, where the 0/1 stands for either grab an item or don’t grab it; items cannot be split or repeated.

There are special subcases of this instance of the problem worth to be analyzed

All items have the same weight

In this case we must simply maximize the profit since all elements weigh the same. Sorting the elements by value and grabbing each time the greatest will solve the problem and thus the greedy algorithm seen some paragraphs before can be used to solve this particular instance of the knapsack problem.

All items have the same value

If all items have the same value we should just try to pack as many items as we can into the knapsack. That means sorting the items by size and grabbing the smallest each time until no more items fit into the knapsack. This is another special instance as the same-weight one that can be solved via a greedy approach sorting by weight.

Subset sum problem - All items have a price proportioned to their size

This is a common instance of the problem similar to having a price-per-kilogram. Imagine a set of gold weights: the heaviest the weight is, the most precious it is. This also means that we can represent the set of elements with just a single array and that we get the maximum benefit if we can entirely fill the knapsack capacity and minimize the free left space in the knapsack. Other instances of this problem are related to reaching a given number C as close as possible with a set of elements. This problem can not be solved via a greedy approach since it is NP-complete (i.e. we can reduce other NP problems to this one but no known polynomial time algorithm exists.. unless until P=NP is proved). This problem is often referred to as the subset sum problem.

Finding a subset of numbers that adds up to a given number \( N \) with a naive approach requires trying out all the possible subsets, i.e. \( 2^N \) attempts and requires an exponential complexity.

A smarter approach makes use of dynamic programming by reusing intermediate solutions for smaller subsets of the native problem. The key to understanding the problem is to understand its recursion. Let us define \( f(i,b) \) as the maximum sum that we can reach with a subset of \( i \) elements and provided that this value is \( \le b \). E.g. given

At every iteration we either grab the \( i_{th} \) element or not enforcing the fact that the maximum value we’ve found must be \( \le b \)

The following program implements the recursion above with a bidimensional memoization table

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

bool ssp(const vector<int>& v, const int& N) {

  vector<vector<int>> m( v.size() + 1 /* 1-based */,
                         vector<int>(N + 1 /* 1-based */, 0) );

  // The line above also took care of the initialization for base
  // cases f(i,0) = 0 and f(0,b) = 0

  for (int i = 1; i <= v.size(); ++i) { // For each subset of elements
    for (int b = 1; b <= N; ++b) { // For each subcapacity
      int opt1 = m[i - 1][b];
      int opt2 = -1;
      if (b - v[i - 1] >= 0) { // No caching to keep this readable
        opt2 = m[i - 1][b - v[i - 1]] + v[i - 1];
        if (opt2 > b)
          opt2 = -1; // Not allowed
      }
      m[i][b] = max(opt1, opt2);
    }
  }

  return (m[v.size()][N] == N);
}

int main() {

  const vector<int> v = { 1, 3, 7, 4 };
  const int N = 11;

  cout << "Subset sum problem can be solved with the given input: "
       << boolalpha << ssp(v, N); // true

  return 0;
}

The complexity of this code is in the order of \( O(N \cdot I) \) where \( I \) is the number of elements in the starting set. This is a pseudopolynomial complexity.

Integer partition problem

The integer partition problem is a special case of the subset problem which asks to partition the elements of the initial set into two subsets \( A \) and \( B \) such that

This is still a NP-complete problem and can be thought of a bin packing problem into two half-sized bins from the original knapsack.

If the input set sums to an even amount, the subsets will have the same \( N \) as sum. If odd, one subset will amount to \( \lfloor N \rfloor \) while the other to \( \lceil N \rceil \) (best-effort).

bool ssp(..) // The same as the previous case

int main() {

  const vector<int> v = { 1, 3, 7, 4, 1 };
  const int N = accumulate(v.begin(), v.end(), 0) / 2;

  cout << "Subset sum problem can be solved with the given input: "
    << boolalpha << ssp(v, N); // true

  return 0;
}

Unbounded knapsack problem

The unbounded knapsack problem is not part of the 0/1 Knapsack class since there is no upper bound on the number of elements (we can grab as many as we want).

The recursion works in a similar way to the so-called Minimum coin change problem with a difference: we’re not interested in the minimum amount of coins but rather in the maximum value we can obtain with a given set of weights by building a recursive set of optimal values at each step (optimal substructure)

with \( w_i \) being the i-th weight and \( v_i \) being the i-th value.

#include <iostream>
#include <vector>
using namespace std;

int ukp(const vector<int>& V, const vector<int>& W, const int& C) {

  vector<int> m(C + 1 /* 1-based */, 0);

  // Base case m[0] = 0 with empty set included above

  for (int c = 1; c <= C; ++c) {
    int max = 0;
    for (int i = 0; i < W.size(); ++i) {

      int w = W[i];
      int v = V[i];

      if (w > c)
        continue;

      int opt = m[c - w] + v;

      if (opt > max)
        max = opt;
    }
    m[c] = max;
  }

  return m[C];
}

int main() {

  const vector<int> v = { 11, 34, 22, 1,  1 };
  const vector<int> w = {  3,  7,  4, 3,  1 };
  const int C = 11;

  cout << "Unbounded knapsack problem solution with the given input: "
    << ukp(v, w, C); // 56

  return 0;
}

The algorithm has \( O(n \cdot W) \) complexity and this doesn’t contradict the NP-completeness statement since \( W \) requires \( \log_{2}{W} \) bits and thus this is a pseudopolynomial complexity.

Unbounded knapsack problem for subset sum

For unbounded knapsack the subset sum problem becomes

Can we fill the knapsack entirely given these elements?

and can be solved again using dynamic programming with a space optimization to just keep track of whether exists a combination (with repetition) of items that guarantees we can sum up to the given value.

#include <iostream>
#include <vector>
using namespace std;

bool uss(const vector<int>& v, const int& N) {

  vector<bool> m(N + 1 /* 1-based */, false);

  for (int b = 1; b <= N; ++b) {
    bool foundZero = false;
    for (int i = 1; i <= v.size(); ++i) {
      bool opt1 = (b - v[i - 1] == 0);
      bool opt2 = false;
      if (b - v[i - 1] >= 0) { // Left expanded for readability
        if (m[b - v[i - 1]] == true)
          opt2 = true;
      }
      foundZero |= opt1 || opt2;
    }
    m[b] = foundZero;
  }

  return (m[N] == true);
}

int main() {

  const vector<int> v = { 3, 7, 4 };
  const int N = 11;

  cout << "Unbounded subset sum problem can be solved with the given input: "
    << boolalpha << uss(v, N); // true

  return 0;
}