Detecting and removing cycle from linked list

Given a singly linked list, detect and remove its cycle (if present)

Given the graph

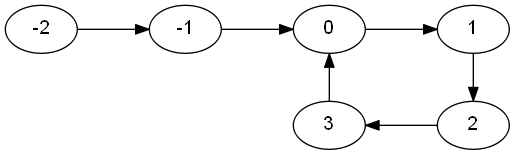
the algorithm needs to find and set to nullptr the node 3’s next pointer.

Floyd’s cycle finding algorithm can be used to detect a cycle in the linked list. In the list pictured above let \( B \) be the preliminary length of the list before the cycle (in the example \( B = 2 \)) and \( C \) be the cycle length (in the example \( C = 4 \)). After \( B \) steps the slow pointer is at node 0 at the beginning of the cycle and the fast pointer is at a node \( r \). Notice that \( r = 2B \) since the fast pointer proceeds in steps of two, the first \( B \) were used to get to the cycle from the beginning while the remaining \( B \) were spent in the cycle with \( r \mod C \equiv B \). If we now consider only the step inside the cycle and proceed to the end of it by adding another \( C - r \) steps to both we have that the slow one ends up in \( C - r \) while the fast one ends up in \( r + 2(C - r) = 2C - r \equiv C - r (\mod C) \) therefore both pointers end up in the same node \( C - r \) .

Now let us suppose that both pointers met at a point in the cycle distant \( k \) nodes from the beginning of it. To find the node that lies at the beginning of the cycle we can move one pointer to the head of the list (unless the head is already the start of the cycle) and try to exhaust the beginning of the list by moving both forward - they will meet at the cycle’s first node. This happens because at the intersection point \( k \) the slow pointer has traveled \( B + k \) while the fast one \( 2 (B + k) = B + k + (C - k) + k \)

Therefore after getting both pointers at the intersection point, if one pointer is placed at the beginning, moving both with equal steps will ensure they meet at the start of the loop.

void detect_and_remove_cycle (Node *root) { // Assumes root != nullptr
  Node *slow = root, *fast = root;

  while (slow && fast) {
    slow = slow->next;
    fast = fast->next;
    if (fast) fast = fast->next;

    if (slow == fast)
      break; // Cycle found
  }

  if (slow != fast || (!slow && !fast))
    return; // No cycle was found or list finished prematurely

  // Remove the cycle
  slow = root;
  if (slow == fast) { // Circular list with no beginning

    fast = fast->next;
    while (fast->next != slow)
      fast = fast->next;

  } else {

    while (slow->next != fast->next) {
      slow = slow->next;
      fast = fast->next;
    }

  }
  fast->next = nullptr;
}

The code is \( O(N) \) and uses constant space.